Задача 80730 ...
Условие
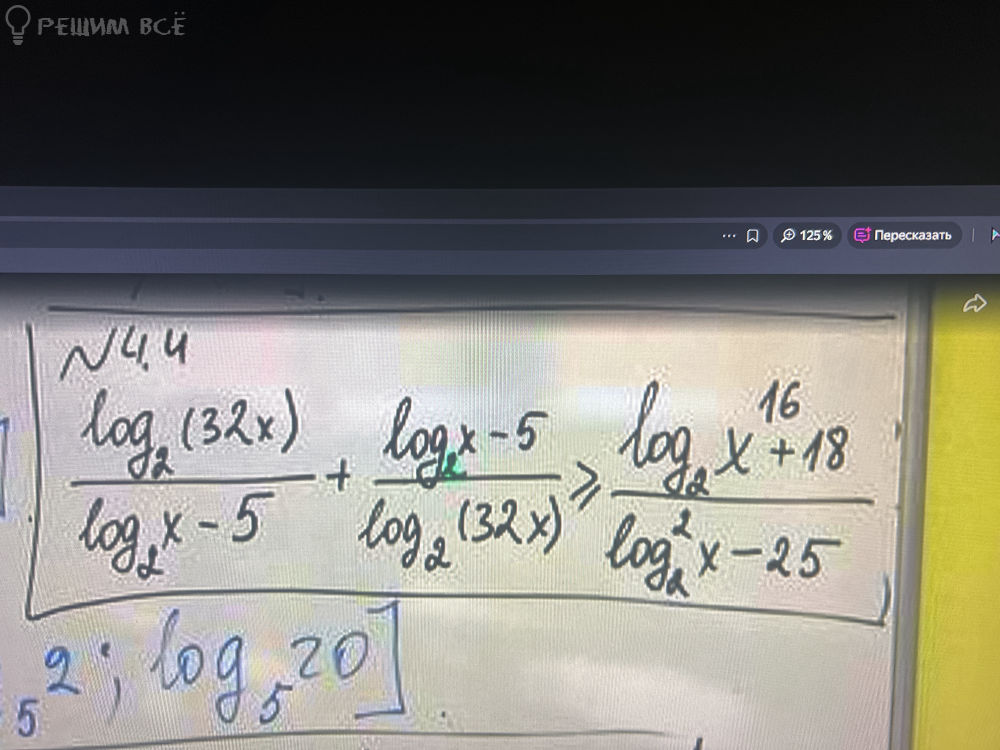
Решение
Заметим, что логарифм произведения равен сумме логарифмов:
[m]\log_2 (32x) = \log_2 x + \log_2 32 = \log_2 x + 5[/m]
Лог. от степени равен степени, умноженной на лог. основания:
[m]\log_2 x^{16} + 18 = 16\log_2 x + 18[/m]
Разность квадратов:
[m]\log_2^2 x - 25 = (\log_2 x - 5)(\log_2 x + 5)[/m]
Подставляем:
[m]\frac{\log_2 x + 5}{\log_2 x - 5} + \frac{\log_2 x - 5}{\log_2 x + 5} ≥ \frac{16\log_2 x + 18}{(\log_2 x - 5)(\log_2 x + 5)}[/m]
Приводим дроби к общему знаменателю и переносим налево:
[m]\frac{(\log_2 x + 5)^2}{(\log_2 x - 5)(\log_2 x + 5)} + \frac{(\log_2 x - 5)^2}{(\log_2 x + 5)(\log_2 x - 5)} - \frac{16\log_2 x + 18}{(\log_2 x - 5)(\log_2 x + 5)} ≥ 0[/m]
[m]\frac{(\log_2 x + 5)^2 + (\log_2 x - 5)^2 - (16\log_2 x + 18)}{(\log_2 x - 5)(\log_2 x + 5)} ≥ 0[/m]
[m]\frac{\log_2^2 x + 10\log_2 x + 25 + \log_2^2 x - 10\log_2 x + 25 - 16\log_2 x - 18}{(\log_2 x - 5)(\log_2 x + 5)} ≥ 0[/m]
[m]\frac{2\log_2^2 x - 16\log_2 x + 32}{(\log_2 x - 5)(\log_2 x + 5)} ≥ 0[/m]
[m]\frac{2(\log_2^2 x - 8\log_2 x + 16)}{(\log_2 x - 5)(\log_2 x + 5)} ≥ 0[/m]
В числителе получился квадрат разности:
[m]\frac{2(\log_2 x - 4)^2}{(\log_2 x - 5)(\log_2 x + 5)} ≥ 0[/m]
Точка, в которой числитель равен 0, является решением:
[m]\log_2 x - 4 = 0[/m]
[m]\log_2 x = 4[/m]
[m]x1 = 2^4 = 16[/m]
Далее, если числитель не равен 0, то он больше 0, потому что квадрат.
Так как левая часть неотрицательна, то знаменатель больше 0.
[m](\log_2 x - 5)(\log_2 x + 5) > 0[/m]
Получаем совокупность (НЕ СИСТЕМУ!) Хотя бы одно из неравенств должно выполняться. Совокупность обозначают квадратной скобкой.
[ log_2 x < -5
[ log_2 x > 5
Решаем:
[ 0 < x < 2^(-5)
[ x > 2^5
Получаем:
x2 ∈ (0; 1/32) U (32; +oo)
Ответ: x ∈ (0; 1/32) U {16} U (32; +oo)