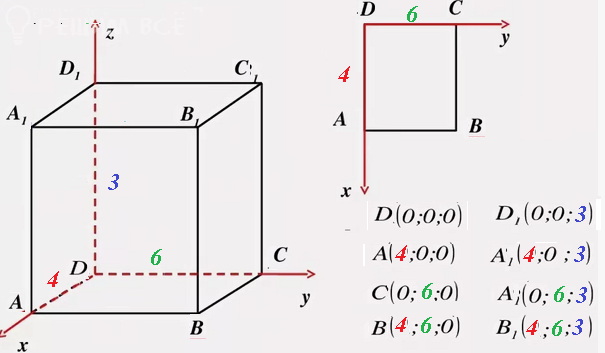
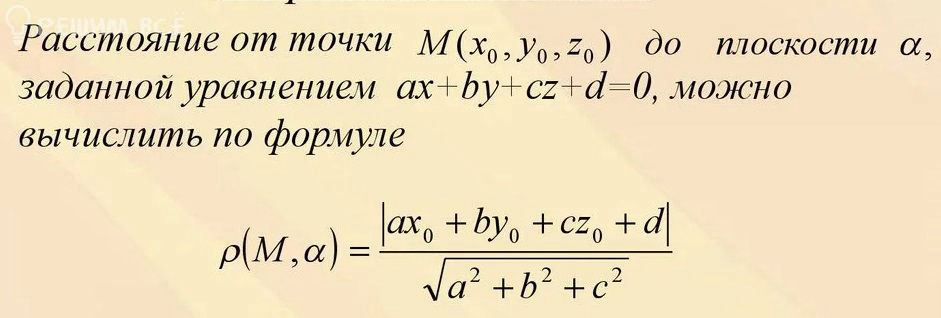Задача 80728 Как выглядит этот квадрат ...
Условие

21
Решение
★
Запишем уравнение плоскости в виде:
ax+by+cz+d=0 (#)
Подставляем координаты точек
D_(1) (0;0;3)
a*x+b*0+c*3+d=0 ⇒ c=-d/3
A(4;0;0)
a*4+b*0+c*0+d=0 ⇒ a=-d/4
C(0;6:0)
a*0+b*6+c*0+d=0 ⇒ b=-d/6
Тoгда уравнение (#) примет вид:
(-d/4)x+(-d/6)y+(-d/3)z+d=0
Cокращаем на d и умножаем на (-12)
[b]3x+2y+4z-12=0[/b]
Тогда по формуле (см. скрин 2)
ρ (B; α) =|3*4+2*6+4*0-12|/sqrt(3^2+2^2+4^2)=[b]12/sqrt(29)[/b]