Задача 80725 Помогите решить уравнения по...
Условие
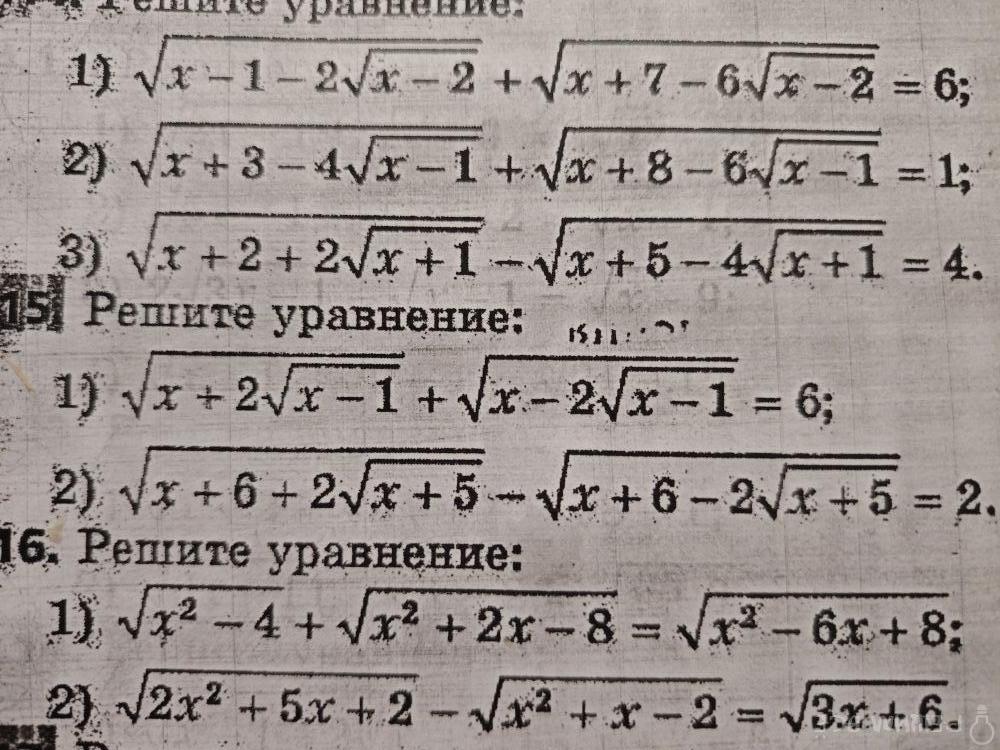
Решение




Все решения
Сделаем замену: [m]t = \sqrt{x+5}[/m], тогда [m]x+6 = t^2 + 1[/m]
Надеюсь, понятно, почему так.
Заметим, что t ≥ 0, потому что корень арифметический, то есть неотрицательный.
И при этом x ≥ -5.
[m]\sqrt{t^2 + 1 + 2t} - \sqrt{t^2 + 1 - 2t} = 2[/m]
[m]\sqrt{(t + 1)^2} - \sqrt{(t - 1)^2} = 2[/m]
Как известно, [m]\sqrt{a^2} = |a|[/m], поэтому получается:
[m]|t + 1| - |t - 1| = 2[/m]
Так как t ≥ 0, то t + 1 > 0, |t + 1| = t + 1.
А вот с |t - 1| возможно два варианта:
1) t ∈ [0; 1), то есть t - 1 < 0, тогда |t - 1| = 1 - t
[m]t + 1 - (1 - t) = 2[/m]
[m]t + 1 - 1 + t = 2[/m]
[m]2t = 2[/m]
[m]t = 1[/m], но по условию t < 1, поэтому решений нет.
2) t ≥ 1, тогда |t - 1| = t - 1
[m]t + 1 - (t - 1) = 2[/m]
[m]t + 1 - t + 1 = 2[/m]
[m]2 = 2[/m]
Это истинное равенство, оно верно при любом t ≥ 1
Возвращаемся к переменной x:
[m]t = \sqrt{x+5} ≥ 1[/m]
[m]x + 5 ≥ 1[/m]
[m]x ≥ -4[/m]
Ответ: x ∈ [-4; +oo)