Задача 80724 Решите пожалуйста, алгебра 9 класс ...
Условие

Решение
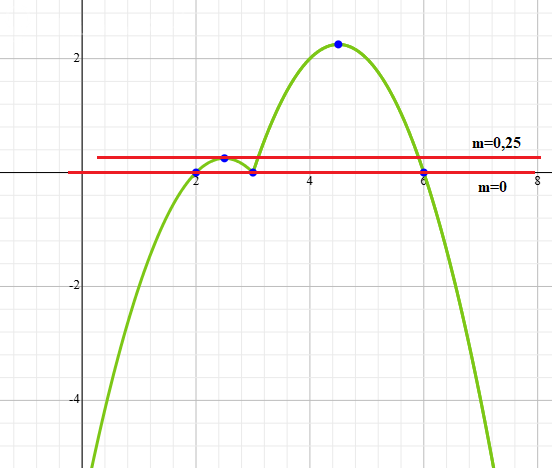
График показан на рисунке.
График распадается на две параболы.
При x < 3 будет |x - 3| = 3 - x, тогда:
y1 = 2(3 - x) - x^2 + 7x - 12
y1 = -x^2 + 5x - 6
Вершина этой параболы:
x01 = -b/(2a) = -5/(-2) = 2,5
y01 = -(2,5)^2 + 5*2,5 - 6 = -6,25 + 12,5 - 6 = 0,25
При x ≥ 3 будет |x - 3| = x - 3, тогда:
y2 = 2(x - 3) - x^2 + 7x - 12
y2 = -x^2 + 9x - 18
Вершина этой параболы:
x02 = -b/(2a) = -9/(-2) = 4,5
y02 = -(4,5)^2 + 9*4,5 - 18 = -20,25 + 40,5 - 18 = 2,25
Точка пересечения этих парабол:
-x^2 + 5x - 6 = -x^2 + 9x - 18
5x - 6 = 9x - 18
18 - 6 = 9x - 5x
4x = 12
x0 = 3, y0 = 2*|3 - 3| - 3^2 + 7*3 - 12 = 2*0 - 9 + 21 - 12 = 0
Значит, при m = 0 прямая y = m будет пересекать график функции в 3 точках.
Так как ветви обеих парабол направлены вниз, и при этом
y02 > y01, то при m = y01 = 0,25 прямая y = m будет пересекать график функции в 3 точках.
Ответ: m1 = 0; m2 = 0,25