Задача 80723 Исследовать функцию и построить ее...
Условие
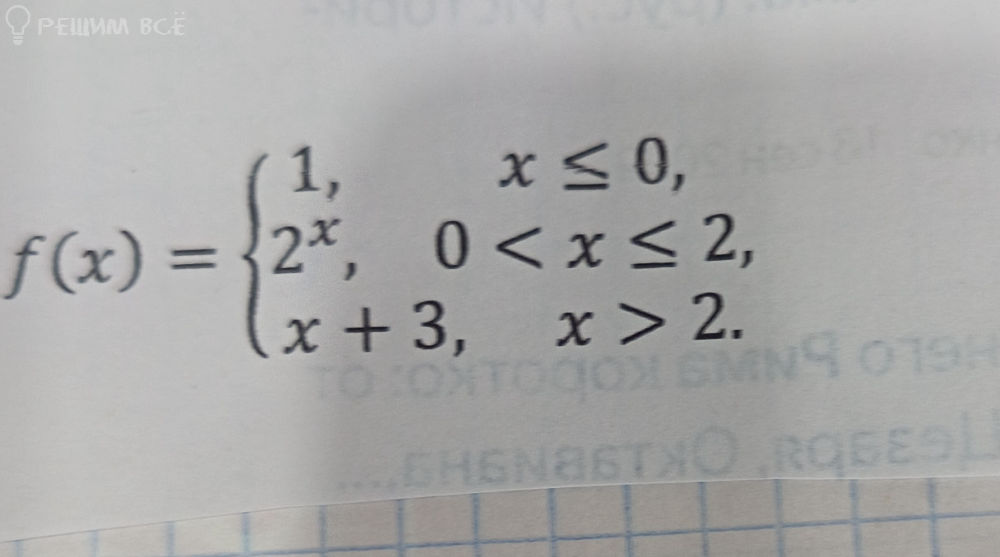
Решение
1,\ x ≤ 0 \\
2^{x},\ 0 < x ≤ 2 \\
x+3,\ x > 2 \\
\end{cases}[/m]
Схема исследования функции:
1. Найти область определения. Выделить особые точки (точки разрыва).
Функция кусочно-непрерывная, x ∈ (-oo; +oo).
Проверим значения на концах интервалов.
[m]\lim \limits_{x \to 0-0} y = \lim \limits_{x \to 0-0} 1 = 1[/m]
[m]\lim \limits_{x \to 0+0} y = \lim \limits_{x \to 0+0} 2^{x} = 2^0 = 1[/m]
В точке x = 0 разрыва нет.
[m]\lim \limits_{x \to 2-0} y = \lim \limits_{x \to 2-0} 2^{x} = 2^2 = 4[/m]
[m]\lim \limits_{x \to 2+0} y = \lim \limits_{x \to 2+0} (x+3) = 2+3 = 5[/m]
В точке x = 2 неустранимый разрыв 1 рода - скачок функции.
2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
Вертикальных асимптот нет.
3. Найти точки пересечения с осями координат и промежутки знакопостоянства.
y(0) = 1 - точка пересечения с осью Oy.
С осью Ox пересечений нет, y > 0 при любом x ∈ (-oo; +oo)
4. Определить, является ли функция чётной или нечётной.
Не четная и не нечетная.
5. Определить, является ли функция периодической.
Не периодическая.
6. Найти точки экстремума и интервалы возрастания-убывания.
Точки экстремума - это точки, в которых y' = 0 или не существует.
y'(x ≤ 0) = 1' = 0 - но это не экстремум, это график параллелен оси Ox.
y'(0 < x ≤ 2) = (2^(x))' = 2^(x) * ln 2 > 0 при любом x ∈ (0; 2].
y'(x > 2) = (x + 3)' = 1 > 0 при любом x > 2.
График экстремумов не имеет.
7. Найти точки перегиба и интервалы выпуклости-вогнутости.
Точки перегиба - это точки, в которых y'' = 0 или не существует.
y''(x ≤ 0) = 0' = 0 - но это не перегиб, это стационарность.
y''(0 < x ≤ 2) = (2^(x) * ln 2)' = 2^(x) * (ln 2)^2 > 0 при любом x ∈ (0; 2].
y'(x > 2) = (1)' = 0, но это тоже не перегиб, а стационарность.
График точек перегиба не имеет.
При всех x график вогнутый (выпуклый вниз) или прямой.
8. Найти наклонные асимптоты. Исследовать поведение на бесконечности.
При y < 0 асимптота y = 1, При y > 2 асимптота y = x + 3.
9. Выбрать дополнительные точки и вычислить их координаты (при необходимости).
Дополнительных точек нет.
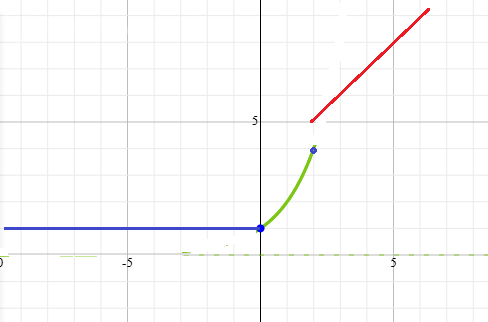
10. Построить график функции, ее асимптот, отметить ключевые точки.
График показан на рисунке.