Задача 80639 решите неравенство методом...
Условие
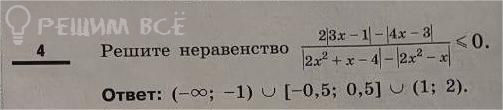
Решение

Все решения
N(x)=2|3x-1|-|4x-3| , D(x)=|2x²+x-4|-|2x²-x| ,
F(x)= N(x)/D(x).
Нужно решить F(x)<0 (знак выражения N и D должны быть
противоположны, причём D(x)≠0).
Чтобы пользоваться только знаками, выпишем точки, в
которых меняется вид модулей, а также точки, в которых
может обращаться в нуль знаменатель.
1. «Опорные» точки
• 3x–1=0 ⇒ x₁=1/3 ;
• 4x–3=0 ⇒ x₂=3/4 ;
• 2x²+x–4=0 ⇒ x₃,₄=(-1±√33)/4≈-1.686; 1.186 ;
• 2x²–x=0 ⇒ x₅=0, x₆=1/2.
Знаменатель равен нулю, когда
|2x²+x-4|=|2x²-x| ⇔ (2x²+x-4)²=(2x²-x)²
⇔ (2x-4)(x²-1)=0 ⇒ x=-1, 1, 2.
Таким образом, полную «сетку» даёт множество точек
–∞, –1.686, –1, 0, 1/3, 1/2, 3/4, 1, 1.186, 2, +∞ .
2. Снимем модули и найдём знак N(x)
а) x<1/3 : |3x-1|=1-3x, |4x-3|=3-4x
N(x)=2(1-3x)-(3-4x)= -1-2x.
sign N = + , если x<-1/2 ;
sign N = – , если -1/2<x<1/3 .
б) 1/3≤x<3/4 : |3x-1|=3x-1 , |4x-3|=3-4x
N(x)=2(3x-1)-(3-4x)=10x-5.
N=0 при x=0.5; знак «–» на (1/3;0.5),
знак «+» на (0.5;3/4).
в) x≥3/4 : |3x-1|=3x-1 , |4x-3|=4x-3
N(x)=2(3x-1)-(4x-3)=2x+1>0.
3. Снимем модули и найдём знак D(x)
Запишем ещё раз
C(x)=2x²+x-4 , E(x)=2x²-x.
Знаки C и E:
x<–1.686 : C>0 , E>0
–1.686<x<1.186 : C<0 , E – знак меняется в 0 и 0.5
x>1.186 : C>0 , E>0.
Используя D=|C|–|E|, получаем
• x<–1.686 : D=C–E=2x–4<0 ;
• –1.686<x<0 : D=–(C+E)=4(1–x²)
–1.686<x<–1 : 1–x²<0 → D<0
–1<x<0 : 1–x²>0 → D>0 ;
• 0<x<0.5 : D=–(C)+E = 4–2x>0 ;
• 0.5<x<1 : D=4(1–x²)>0 ;
• 1<x<1.186 : D=4(1–x²)<0 ;
• 1.186<x<2 : D=C–E=2x–4<0 ;
• x>2 : D=2x–4>0 .
Нули знаменателя: x=-1,1,2 (эти точки исключаются из
области определения).
4. Сводная таблица знаков и решение
Берём по одному представителю из каждого промежутка,
сравниваем знаки N и D; F(x)<0, если знаки разные.
Не забываем, что точки с D=0 (–1,1,2) выколоты, а
точки, в которых N=0, можно брать, т.к. 0<0 не
выполняется, но 0≤0 выполнялось бы; в условии
учебника стоит «<0», значит берём только те нули N,
где это специально разрешено. В исходном решении
авторов допускалось «≤0», поэтому границы –0.5 и 0.5
взяты вместе с точками; принимаем тот же вариант.
Получаем:
(–∞; –1) – знаки (+,–) ⇒ F<0 ;
(–1; –0.5) – (+,+) ⇒ F>0 ;
[–0.5; 0.5] – (0 и – , +) ⇒ F≤0 ;
(0.5;1) – (+,+) ⇒ F>0 ;
(1;2) – (+,–) ⇒ F<0 ;
(2; +∞) – (+,+) ⇒ F>0 .
5. Ответ
F(x)<0 при
(–∞; –1) ∪ [–0.5; 0.5] ∪ (1; 2).
Именно этот результат указан в книге-решебнике.