Задача 80626 ...

69383d1ba0211e4a1fadcf4e

12/9/2025 3:15:54 PM

используя метод введения вспомогательного аргумента решите неравенство √3cos2x+sin2x<1

626fab9a354ab65fb2f43abb

12/9/2025 4:34:14 PM

★

sqrt(3) cos 2x + sin 2x < 1
Вынесем за скобки 2:
2(cos 2x*sqrt(3)/2 + sin 2x*1/2) < 1
Вводим дополнительный аргумент π/6:
2(cos 2x cos π/6 + sin 2x sin π/6) < 1
В скобках стоит формула косинуса разности
2cos (2x - π/6) < 1
cos (2x - π/6) < 1/2
Вводим замену: 2x - π/6 = t
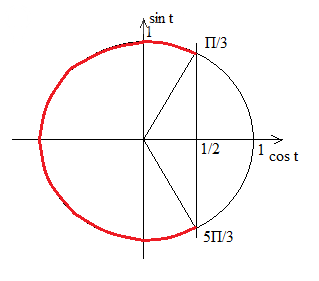
cos t < 1/2
Решение этого неравенства показано на рисунке.
t ∈ (π/3 + 2π*k; 5π/3 + 2π*k), k ∈ Z
Обратная замена:
2x - π/6 ∈ (π/3 + 2π*k; 5π/3 + 2π*k), k ∈ Z
Прибавляем π/6:
2x ∈ (π/3 + π/6 + 2π*k; 5π/3 + π/6 + 2π*k), k ∈ Z
2x ∈ (π/2 + 2π*k; 11π/6 + 2π*k), k ∈ Z
Делим на 2:
x ∈ (π/4 + π*k; 11π/12 + π*k), k ∈ Z