Задача 80620 под а) я сделал уже, хотелось бы только...
Условие

Решение
4(x^2 - 4x + 4) - 16 + (y^2 - 4y + 4) - 4 = 0
4(x - 2)^2 + (y - 2)^2 = 4
[m]\frac{(x-2)^2}{1} + \frac{(y-2)^2}{4} = 1[/m]
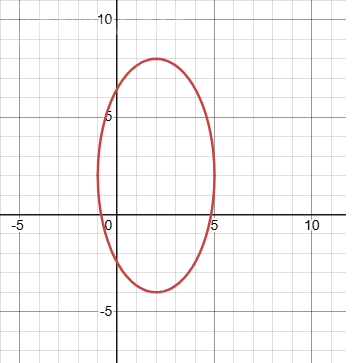
Это эллипс с центром A(2, 2) и полуосями a = 1, b = 2.
Так как b > a, то эллипс - вертикальный.
Параметр c = sqrt(b^2 - a^2) = sqrt(2^2 - 1^2) = sqrt(3)
Координаты фокусов F1(X(A); Y(A) - c); F2(X(A); Y(A) + c)
В нашем случае:
F1(2; 2 - sqrt(3)); F2(2; 2 + sqrt(3))
Эксцентриситет ε = c/b = sqrt(3)/2
б) 7x^2 - 12xy - 2y^2 = 50
Записываем уравнение в полном виде:
A*x^2 + 2B*xy + C*y^2 + 2D*x + 2E*y + F = 0
7x^2 + 2*(-6)*xy + (-2)y^2 + 0x + 0y - 50 = 0
A = 7, B = -6, C = -2, D = 0, E = 0, F = -50
Вычисляем инварианты:
S = A + C = 7 - 2 = 5
[m] δ = \begin{vmatrix}
A & B \\
B & C \\
\end{vmatrix} = \begin{vmatrix}
7 & -6 \\
-6 & -2 \\
\end{vmatrix} = 7(-2) - (-6)(-6) = -14 - 36 = -50[/m]
[m] Δ = \begin{vmatrix}
A & B & D \\
B & C & E \\
D & E & F \\
\end{vmatrix} = \begin{vmatrix}
7 & -6 & 0 \\
-6 & -2 & 0 \\
0 & 0 & -50 \\
\end{vmatrix} =[/m]
[m]= -50 \cdot \begin{vmatrix}
7 & -6 \\
-6 & -2 \\
\end{vmatrix} = -50 \cdot (-50)[/m]
Его даже не надо вычислять, так и оставим.
Составляем систему уравнений:
[m]\begin{cases}
A1 + C1 = S \\
A1 \cdot C1 = δ \\
A1 \cdot C1 \cdot F1 = Δ \\
\end{cases} ⇒ \begin{cases}
A1 + C1 = 5 \\
A1 \cdot C1 = -50 \\
A1 \cdot C1 \cdot F1 = -50 \cdot (-50) \\
\end{cases}[/m]
Из 2 и 3 уравнений сразу получаем:
F1 = -50
1 и 2 уравнения составляют теорему Виета для квадратного:
x^2 - 5x - 50 = 0
(x - 10)(x + 5) = 0
x1 = A1 = 10; x2 = C1 = -5
Получили новое уравнение:
A1*x'^2 + C1*y'^2 + F1 = 0
10x'^2 - 5y'^2 - 50 = 0
10x'^2 - 5y'^2 = 50
x'^2/5 - y'^2/10 = 1
Это гипербола с центром O(0; 0) и полуосями a = sqrt(5), b = sqrt(10)
Параметр c = sqrt(a^2 + b^2) = sqrt(5 + 10) = sqrt(15)
Фокусы F1(-c; 0); F2(c; 0)
В нашем случае F1(-sqrt(15); 0); F2(sqrt(15); 0)
Эксцентриситет ε = c/a = sqrt(15)/sqrt(5) = sqrt(3)
Графики обеих кривых смотрите на рисунках.