Задача 80557 ...
Условие
S(t) = {
sin²(t/2), t ∈ [0; π],
1, t ∈ (π; 5],
1 + (t - 5)², t ∈ (5; 6],
где S(t) — путь в метрах, t — время в секундах.
Построить график функции S(t). Найти:
1) зависимость скорости движения от времени и построить график этой зависимости;
2) скорость движения в момент t₁ = 4 сек, t₂ = 6 сек;
3) среднюю скорость в отрезке t ∈ [4; 6];
4) интервал времени, в течение которого точка находилась в покое;
5) момент времени, когда точка имела наибольшую скорость.
Решение
[m]\large S = \begin{cases}
\sin^2 \frac{t}{2},\ \ \ t ∈ [0; \pi] \\
\ \ \ \ \ \ \ \ 1,\ \ \ t ∈ (\pi; 5] \\
1 + (t - 5)^2, t ∈ (5; 6] \\
\end{cases}[/m]
График движения смотрите на Рисунке 1.
1) Скорость - это производная от пути по времени.
[m]\large v = \begin{cases}
2\sin \frac{t}{2} \cos \frac{t}{2} \cdot \frac{1}{2} = \frac{\sin t}{2},\ \ \ t ∈ [0; \pi] \\
\ \ \ \ \ \ \ \ 0,\ \ \ t ∈ (\pi; 5] \\
2(t - 5), t ∈ (5; 6] \\
\end{cases}[/m]
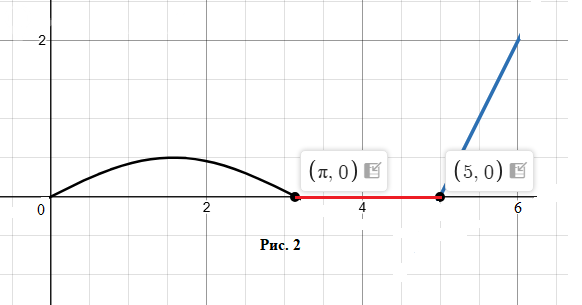
График скорости смотрите на Рисунке 2.
2) v(4) = 0 (м/с), так как 4 ∈ (π; 5]
v(6) = 2(6 - 5) = 2 (м/с), так как 6 ∈ (5; 6]
3) Средняя скорость на отрезке t ∈ [4; 6]
Средняя скорость - это всё пройденное расстояние, делённое на всё затраченное время.
С t = 4 до t = 5 точка стояла на месте.
В t = 5 координата точки равнялась 1, а в t = 6 координата равнялась 2.
Значит, за эти 2 секунды, с t = 4 до t = 6 точка прошла s = 1 м.
Средняя скорость равна ~v = 1/2 = 0,5 (м/с)
4) Точка находилась в покое с t = π до t = 5. Интервал равен 5 - π (с).
5) Точка имела наибольшую скорость в момент t = 6 (с). v(6) = 2 (м/с)