Задача 80556 Помогите с задачами: 1.5, 1.9 , 1.14...
Условие
А также с номером 3
Решение
[m]\large y' = \frac{1}{3} \cdot (\frac{1}{\cos^2 x} - (-\frac{1}{\sin^2 x})) = \frac{1}{3} \cdot (\frac{1}{\cos^2 x} + \frac{1}{\sin^2 x}) = [/m]
[m]\large = \frac{1}{3} \cdot \frac{\sin^2 x + \cos^2 x}{\sin^2 x \cdot \cos^2 x} = \frac{1}{3} \cdot \frac{1}{\sin^2 x \cdot \cos^2 x}[/m]
1.9. [m]\large y = \frac{2}{ctg^3\ x} = 2tg^3\ x[/m]
[m]\large y' = 2 \cdot 3tg^2\ x \cdot \frac{1}{\cos^2 x} = \frac{6tg^2\ x}{\cos^2 x}[/m]
1.14. [m]\large y = \lg^3 (x^2 + 2x + 3)[/m]
[m]\large y' = 3 \lg^2 (x^2 + 2x + 3) \cdot \frac{1}{\ln 10(x^2 + 2x + 3)} \cdot (2x + 2) =[/m]
[m]\large = \frac{3 (2x + 2) \lg^2 (x^2 + 2x + 3)}{\ln 10(x^2 + 2x + 3)}[/m]
1.15. [m]\large \begin{cases}
x = e^{2t} \\
y = cos^2 t \\
\end{cases}[/m]
Производная от функции, заданной параметрически.
Берем производные от x и от y по t:
[m]\large \frac{dx}{dt} = 2e^{2t}[/m]
[m]\large \frac{dy}{dt} = 2\cos t \cdot (-\sin t) = -\sin 2t[/m]
Производная от y по x вычисляется по формуле:
[m]\large y' = \frac{dy}{dx} = \frac{dy}{dt} : \frac{dx}{dt} = \frac{-\sin 2t}{2e^{2t}}[/m]
1.16. [m]\large tg\ (y+ \frac{\pi}{4}) = xy + \frac{\pi x}{4}[/m]
Производная от функции, заданной неявно.
Берем производную от левой и правой частей:
[m]\large \frac{1}{\cos^2(y + \pi/4)} \cdot y' = 1y + xy' + \frac{\pi}{4}[/m]
Выделяем y':
[m]\large y' \cdot (\frac{1}{\cos^2(y + \pi/4)} - x) = y + \frac{\pi}{4}[/m]
Вычисляем y':
[m]\large y' = \frac{y + \pi/4}{\frac{1}{\cos^2(y + \pi/4)} - x} = \frac{(y + \pi/4)\cos^2(y + \pi/4)}{1 - x\cos^2(y + \pi/4)}[/m]
1.17. [m]\large y = (1 + \ln x)^{arctg\ x}[/m]
Производная от функции вида [m]\large y = f(x)^{g(x)}[/m]
Берется как сумма показательной и степенной функций.
[m]y' = (1 + \ln x)^{arctg\ x} \cdot \ln (1 + \ln x) \cdot (arctg\ x)' +[/m]
[m]+ arctg\ x \cdot (1 + \ln x)^{arctg\ x - 1} \cdot (1 + \ln x)'[/m]
[m]y' = (1 + \ln x)^{arctg\ x} \cdot \ln (1 + \ln x) \cdot \frac{1}{1+x^2} + [/m]
[m]+ arctg\ x \cdot (1 + \ln x)^{arctg\ x - 1} \cdot \frac{1}{x}[/m]
[m]y' = (1 + \ln x)^{arctg\ x} \cdot (\frac{\ln (1 + \ln x)}{1+x^2} + \frac{arctg\ x}{x(1 + \ln x)})[/m]
3. [m]\large y = e^{-2x}[/m]; M(-1; e^2)
Уравнение касательной:
f(x) = y(x0) + y'(x0)*(x - x0)
[m]\large y' = -2e^{-2x}[/m]
[m]\large y'(x0) = y'(-1) = -2e^{2}[/m]
Уравнение касательной:
[m]\large f(x) = e^2 - 2e^2(x + 1)[/m]
[m]\large f(x) = e^2 - 2e^2 \cdot x - 2e^2[/m]
[m]\large f(x) = -2e^2 \cdot x - e^2[/m]
Нормаль - это прямая, перпендикулярная к касательной в той же точке.
Уравнение нормали:
[m]n(x) = y(x0) + k2 \cdot (x - x0)[/m]
Если две прямые перпендикулярны, то произведение их коэффициентов:
k1*k2 = -1
k1 = -2e^2, значит, k2 = 1/2*e^(-2)
[m]\large n(x) = e^2 + 0,5e^{-2}(x + 1)[/m]
[m]\large n(x) = e^2 + 0,5e^{-2} \cdot x + 0,5e^{-2} [/m]
[m]\large n(x) = 0,5e^{-2} \cdot x + e^2 + 0,5e^{-2} [/m]
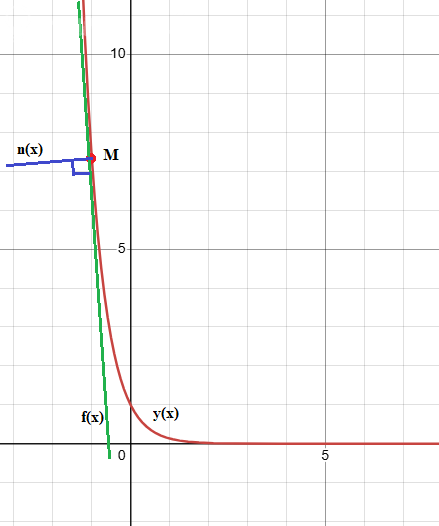
График прилагается. Так как функция y = e^(-2x) убывает на всем промежутке (-oo; +oo), то производная y'(x) < 0 при любом x.
Касательная f(x) показана зеленым цветом, а нормаль n(x) - синим.
Нормаль традиционно начинается в точке касания и идет наружу графика.