Задача 80548 реши...
Условие
[m]
\frac{\log_{8}x}{\log_{8}\left(\frac{x}{64}\right)} \geq \frac{2}{\log_{8}x} + \frac{3}{\log_{8}^{2}x - \log_{8}x^{2}}.
[/m]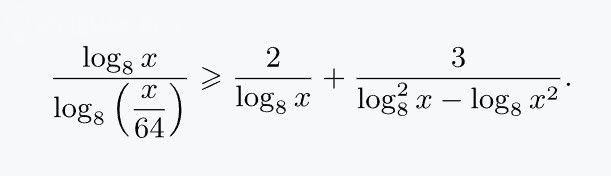
Решение
{x>0
{[m]log_{8}x ≠ 0 ⇒ x ≠ 1[/m]
{[m]log_{8}\frac{x}{64} ≠ 0[/m] ⇒ [m]\frac{x}{64} ≠ 1[/m] ⇒ [m]x ≠ 64[/m]
{[m]log^2_{8}x-log_{8}x^2≠ 0[/m] ⇒[m]log^2_{8}x-2log_{8}x≠ 0[/m] ⇒ [m]log_{8}x ≠ 0[/m] и [m]log_{8}x-2 ≠ 0[/m] ⇒ [m]x ≠ 1[/m] и [m]x ≠ 64[/m]
ОДЗ: (0;1) U (1;64)U(64;+ ∞ )
[i]Замена переменной[/i]:
[m]log_{8}x=t[/m]
[m]\frac{t}{t-2}\geq \frac{2}{t}+\frac{3}{t^2-2t}[/m]
[m]\frac{t}{t-2}- \frac{2}{t}-\frac{3}{t(t-2)}\geq0[/m]
[m]\frac{t^2-2(t-2)-3}{t(t-2)}\geq 0[/m]
[m]\frac{t^2-2t+1}{t(t-2)}\geq 0[/m]
[m]\frac{(t-1)^2}{t(t-2)}\geq 0[/m]
Решаем методом интервалов:
___+___ (0) _-__ [1] __-__ (2) ___+___
t < 0 или t=1 или t>2
Обратный переход в переменной х:
[m]log_{8}x<0[/m] или [m]log_{8}x=1[/m] или [m]log_{8}x> 2[/m]
[m] x < 1[/m] или [m]x=8[/m] или [m]log_{8}x>log_{8}64[/m] ⇒[m] x>64[/m]
C учетом ОДЗ:
О т в е т. (0; 1) U{8}U(64;+ ∞ )