Задача 80525 Привести уравнение линии второго порядка...
Условие
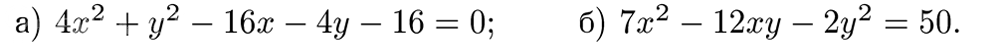
Решение
Это несложное упражнение.
(4x^2 - 16x) + (y^2 - 4y) = 16
4(x^2 - 4x + 4) - 16 + (y^2 - 4y + 4) - 4 = 16
4(x - 2)^2 + (y - 2)^2 = 16 + 16 + 4
4(x - 2)^2 + (y - 2)^2 = 36
(x - 2)^2/9 + (y - 2)^2/36 = 1
Это эллипс с центром A(2; 2) и полуосями a = 3; b = 6
Смотрите Рисунок 1.
2) 7x^2 - 12xy - 2y^2 = 50
Это намного сложнее, нам надо избавиться от члена 12xy.
Запишем уравнение в общем виде со всеми коэффициентами:
7x^2 - 12xy - 2y^2 + 0x + 0y - 50 = 0
Применим метод инвариантов. Коэффициенты уравнения:
A = 7; 2B = -12; C = -2; D = 0; E = 0; F = -50
[m]S = A + C = 7 - 2 = 5[/m]
[m]\delta = \begin{vmatrix}
A & B \\
B & C \\
\end{vmatrix} = \begin{vmatrix}
7 & -6 \\
-6 & -2 \\
\end{vmatrix} = 7(-2) - (-6)(-6) = -14 - 36 = -50[/m]
[m]\Delta = \begin{vmatrix}
A & B & D \\
B & C & E \\
D & E & F \\
\end{vmatrix} = \begin{vmatrix}
7 & -12 & 0 \\
-12 & -2 & 0 \\
0 & 0 & -50 \\
\end{vmatrix} = [/m]
[m]= -50 \cdot \begin{vmatrix}
7 & -12 \\
-12 & -2 \\
\end{vmatrix} = (-50)(-50)[/m]
Составим систему:
[m]\begin{cases}
A1 + C1 = S \\
A1 \cdot C1 = \delta \\
A1 \cdot C1 \cdot F1 = \Delta \\
\end{cases} ⇒ \begin{cases}
A1 + C1 = 5 \\
A1 \cdot C1 = -50 \\
A1 \cdot C1 \cdot F1 = (-50)(-50) \\
\end{cases}[/m]
Из 2 и 3 уравнения сразу получаем:
[b]F1 = -50[/b]
1 и 2 уравнения решаем по теореме Виета:
{ A1 + C1 = 5
{ A1*C1 = -50
[b]A1 = 10; C1 = -5[/b]
Новое уравнение:
10x'^2 - 5y'^2 - 50 = 0
10x'^2 - 5y'^2 = 50
x'^2/5 - y'^2/10 = 1
Можно и другим, более общим способом решить.
Для этого нужно повернуть оси на угол а по формулам:
{ x = x'*cos a - y'*sin a
{ y = x'*sin a + y'*cos a
Подставляем:
7(x'*cos a - y'*sin a)^2 - 12(x'*cos a - y'*sin a)(x'*sin a + y'*cos a) -
- 2(x'*sin a + y'*cos a)^2 = 50
7(x'^2*cos^2 a - 2*x'*y'*sin a*cos a + y'^2*sin^2 a) -
- 12(x'^2*sin a*cos a - x'*y'*sin^2 a + x'*y'*cos^2 a - y'^2*sin a*cos a) -
- 2(x'^2*sin^2 a + 2x'*y'*sin a*cos a + y'^2*cos^2 a) = 50
x'^2*(7cos^2 a - 12sin a*cos a - 2sin^2 a) +
+ x'*y'*(-14sin a*cos a + 12sin^2 a - 12cos^2 a - 4sin a*cos a) +
+ y'^2*(7sin^2 a + 12sin a*cos a - 2cos^2 a) = 50
Коэффициент при x'*y' приравниваем к 0, вычисляем угол а.
-14sin a*cos a + 12sin^2 a - 12cos^2 a - 4sin a*cos a = 0
12sin^2 a - 18sin a*cos a - 12cos^2 a = 0
Делим всё уравнение на 6cos^2 a:
2tg^2 a - 3tg a - 2 = 0
Получили квадратное равнение относительно tg a.
D = (-3)^2 - 4*2*(-2) = 9 + 16 = 25 = 5^2
tg a1 = (3 - 5)/(2*2) = -2/4 = -1/2; a = arctg(-1/2) > 90°
tg a2 = (3 + 5)/(2*2) = 8/4 = 2; a = arctg 2 < 90°
Выбираем больший угол.
tg a = -1/2; 90° < a < 180°; sin a > 0; cos a < 0
1/cos^2 a = 1 + tg^2 a = 1 + 1/4 = 5/4
cos^2 a = 4/5
[b]cos a = -2/sqrt(5)[/b]
sin^2 a = 1 - cos^2 a = 1 - 4/5 = 1/5
[b]sin a = 1/sqrt(5)[/b]
Подставляем sin a и cos a в уравнение кривой:
x'^2*(7cos^2 a - 12sin a*cos a - 2sin^2 a) +
+ x'*y'*(-14sin a*cos a + 12sin^2 a - 12cos^2 a - 4sin a*cos a) +
+ y'^2*(7sin^2 a + 12sin a*cos a - 2cos^2 a) = 50
x'^2*(7*4/5 - 12*1/sqrt(5)*(-2/sqrt(5)) - 2*1/5) + x'*y'*0 +
+ y'^2*(7*1/5 + 12*1/sqrt(5)*(-2/sqrt(5)) - 2*4/5) = 50
x'^2*(28/5 + 24/5 - 2/5) + y'^2*(7/5 - 24/5 - 8/5) = 50
x'^2*(50/5) + y'^2*(-25/5) = 50
10x'^2 - 5y'^2 = 50
x'^2/5 - y'^2/10 = 1
Это вертикальная гипербола с центром O(0; 0) и полуосями
a = sqrt(5); b = sqrt(10), повернутая на угол a = arctg (-1/2)
Смотрите Рисунок 2. Новые оси x', y' там тоже показаны.