Задача 80465 ...
Условие
ЗАДАЧИ В ТАБЛИЦАХ
§ 1. Угол между двумя прямыми
КУБ
Таблица 1
1
В единичном кубе A...D₁ найдите угол между прямыми AC и BD.
2
В единичном кубе A...D₁ найдите угол между прямыми CC₁ и AD.
3
В единичном кубе A...D₁ найдите угол между прямыми AA₁ и B₁C.
4
В единичном кубе A...D₁ найдите угол между прямыми BB₁ и A₁C.
5
В единичном кубе A...D₁ найдите угол между прямыми AC₁ и DC₁.
6
В единичном кубе A...D₁ найдите угол между прямыми AD₁ и A₁B.
7
В единичном кубе A...D₁ найдите угол между прямыми DC₁ и D₁B₁.
8
В единичном кубе A...D₁ найдите угол между прямыми AD₁ и BD.
9
В единичном кубе A...D₁ найдите угол между прямыми A₁C₁ и B₁C.
10
В единичном кубе A...D₁ найдите угол между прямыми AC₁ и AD.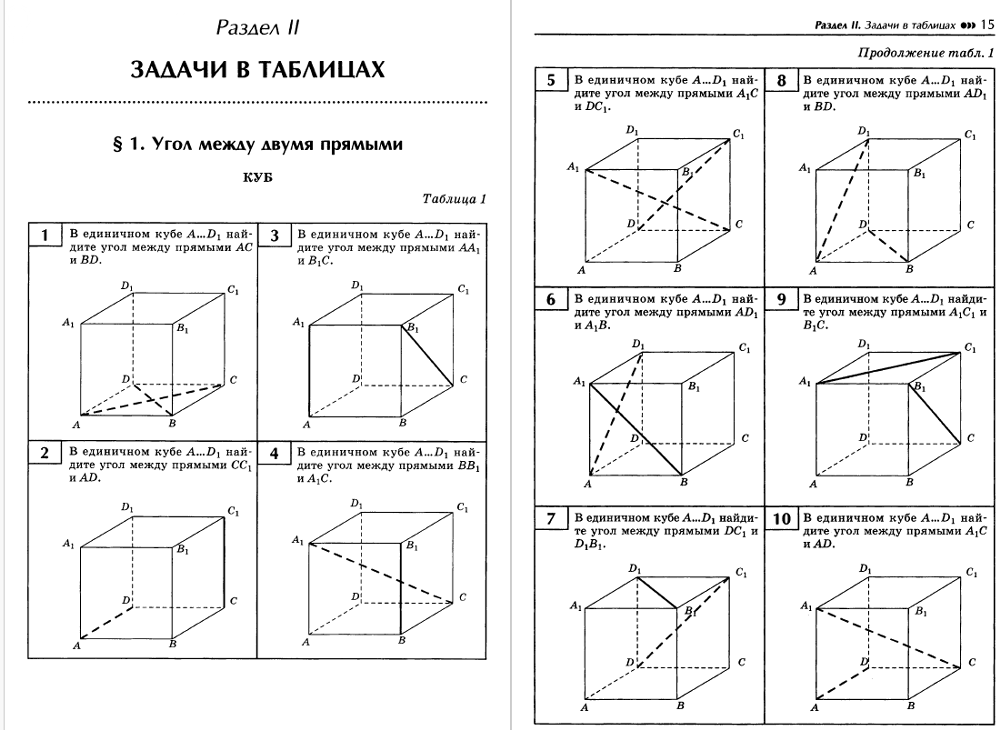
Решение
Надо только помнить, что если перенести один отрезок параллельным переносом, то его угол со вторым отрезком не изменится.
1) Угол между двумя диагоналями в квадрате равен 90°.
2) Переносим ребро CC1 на AA1.
Угол между двумя сторонами одного квадрата равен 90°.
3) Переносим диагональ B1C на A1D.
Угол между стороной квадрата и его диагональю равен 45°.
4) Переносим ребро BB1 на AA1. Получаем треугольник AA1C.
Он прямоугольный, AA1 = 1, A1C = sqrt(3)
cos AA1C = 1/sqrt(3); Угол AA1C ≈ 54,7356° = 54° 44' 08,2''
5) Вот это действительно трудный вопрос. Странно, что он 5, а не 10.
Обычно самые трудные вопросы - это самые последние.
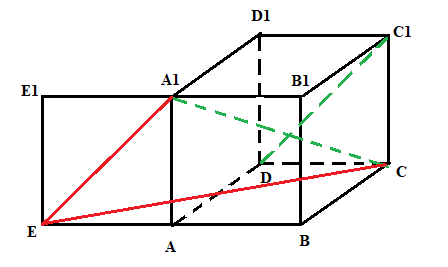
Смотрите рисунок 1. Диагональ грани DC1 и диагональ куба A1C я нарисовал зеленым. Кроме того, я дорисовал грань AA1E1E и параллельно перенес диагональ грани DC1 в диагональ A1E.
Её я показал красным.
Также красным я дорисовал отрезок CE, получив Δ A1CE.
Найдем длины его сторон.
A1E = sqrt(2), A1C = sqrt(3),
CE - это гипотенуза прямоугольного Δ BCE, где BC = 1, BE = 2.
По теореме Пифагора
CE^2 = BC^2 + BE^2 = 1^2 + 2^2 = 5
CE = sqrt(5)
Но по той же теореме Пифагора
A1E^2 + A1C^2 = (sqrt(2))^2 + (sqrt(3))^2 = 2 + 3 = 5 = CE^2
Значит, треугольник A1CE - прямоугольный.
Угол CA1E = 90°
6) Переносим диагональ AD1 в BC1. Дорисовываем диагональ A1C1.
Получили треугольник из трех диагоналей: A1BC1.
Так как это куб, то все диагонали граней - одинаковые.
Значит, Δ A1BC1 - равносторонний.
Угол A1BC1 = BA1C1 = A1C1B = 60°.
7, 8 и 9 задачи - такие же, как 6)
7) Переносим B1D1 на BD.
Угол BDC1 = 60°.
8) Переносим BD на B1D1.
Угол AB1D1 = 60°.
9) Переносим B1C на A1D.
Угол DA1C1 = 60°.
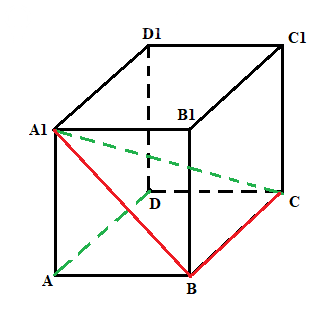
10) Задача аналогична 4 задаче.
Переносим AD на BC и дорисовываем диагональ A1B.
Заданные диагонали AD и A1C я нарисовал зеленым.
Дополненные BC и A1B - красным. Длины сторон Δ A1BC:
BC = 1, A1B = sqrt(2), A1C = sqrt(3)
cos BCA1 = 1/sqrt(3), Угол BCA1 ≈ 54,7356° = 54° 44' 08,2''