Задача 80464 Помогите пожалуйста решить задачу!!!...
Условие
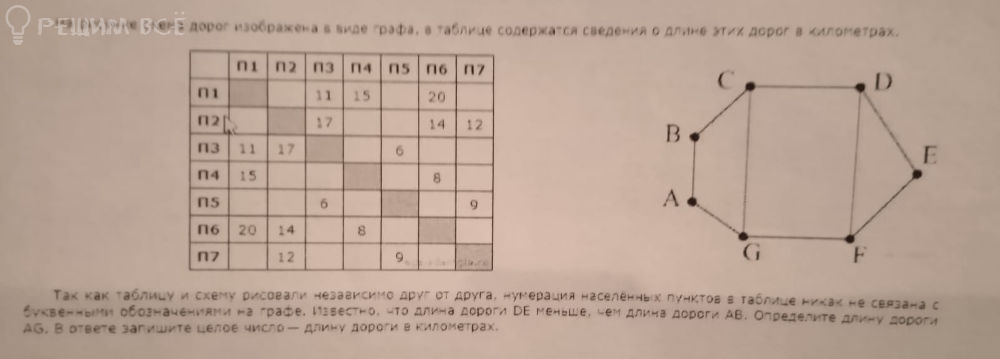
Решение
В строках (и столбцах) П1, П2, П3 и П6 по 3 числа.
Значит, из этих пунктов выходят по 3 дороги.
Им соответствуют на схеме пункты C, D, G, F.
В строках (и столбцах) П4, П5 и П7 по 2 числа.
Значит, из этих пунктов выходят по 2 дороги.
Им соответствуют на схеме пункты A, B, E.
Назовём степенью пункта количество дорог, выходящих из него.
Пункты C, D, G, F имеют степень 3, а пункты A, B, E - степень 2.
Мы знаем, что путь DE, связывающий пункт степени 2 с пунктом степени 3, меньше, чем путь AB, связывающий два пункта степени 2.
Из пунктов степени 3 к пунктам степени 2 выходят дороги:
П1-П4 = 15, П2-П7 = 12, П3-П5 = 6, П6-П4 = 8.
Из пунктов степени 2 к пунктам степени 2 выходят дорога:
П5-П7 = 9.
Значит, П5 и П7 - это пункты A и B. Путь |AB| = 9
Тогда пункты D и E соответствуют П4 и П6.
Потому что путь П6-П4 = 8 < П5-П7 = 9
Хотя путь П3-П5 = 6 < П5-П7 = 9, но он не подходит, потому что в обоих путях повторяется пункт П5, а этого быть не должно.
Очевидно, [b]E = П4[/b] (степень 2), а [b]D = П6[/b] (степень 3).
Пункт П4 кроме П6 связан с П1, значит, [b]F = П1[/b].
Путь |EF| = П4-П1 = 15, путь |FD| = П1-П6 = 20.
Пункт F = П1 кроме пунктов П4 = E и П6 = D связан с пунктом G.
Значит, [b]G = П3[/b]. Путь |FG| = П1-П3 = 11.
Пункт G = П3 связан только с одним пунктом степени 2:
[b]A = П5[/b]. Тогда [b]B = П7[/b].
Смотрим по таблице путь AG.
Ответ: [b]|AG| = П5-П3 = 6[/b]