Задача 80438 ...
Условие
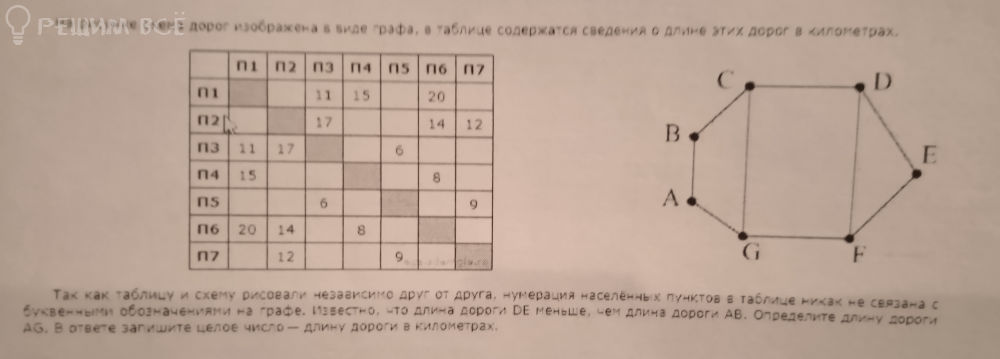
Решение
1. Считываем из таблицы, какие пары пунктов соединены дорогами.
(пункт – «п»)
п1-п3 – 11 км
п1-п4 – 15 км
п1-п7 – 20 км
п2-п3 – 17 км
п2-п5 – 14 км
п2-п7 – 12 км
п3-п4 – 17 км
п4-п5 – 6 км
п5-п6 – 8 км
п6-п7 – 9 км
Всего 9 дорог – ровно столько же, сколько рёбер на рисунке
(семь сторон многоугольника и две внутренние диагонали).
2. Определяем степени вершин (сколько дорог подходит к каждому пункту):
п1 – 3; п2 – 3; п3 – 3; п4 – 3;
п5 – 3; п6 – 2; п7 – 2.
У нас получилось:
• две вершины степени 2 (п6 и п7);
• пять вершин степени 3.
На схеме степени такие:
A – 2, B – 2, E – 2; C, D, F, G – 3.
Значит п6, п7 и ещё одна «тройка» должны отвечать A, B, E.
Из таблицы видно, что две вершины степени 2 соединены между
собой (п6-п7 = 8 км).
На рисунке единственная дорога, соединяющая две «двойки», – это AB.
Следовательно 8 км – это AB.
3. По условию DE < AB.
Из оставшихся дорог единственная, длина которой меньше 8 км, – 6 км.
Следовательно дорога длиной 6 км – это DE,
а участвующие в ней вершины – D и E.
Раз у E степень 2, значит E – это тот «тройочный» пункт,
который ещё не использован. 6 км соответствует ребру п4-п5,
значит {п4, п5} = {D, E}. У п5 степень 3, следовательно
п5 – D, а п4 – E.
4. Осталось расставить C, F, G.
На рисунке G соединён с А, F и C, то есть с одной вершиной степени 2
и двумя вершинами степени 3. В таблице такой же набор даёт именно
п1 (п1 связан с п6 (=A), п4 (=E) и п5 (=D)). Значит п1 – это G.
5. Теперь все вершины расставлены:
A – п6 B – п7 C – п3
D – п5 E – п4 F – п2 G – п1
6. Длина дороги AG – это расстояние между пунктами п6 и п1.
В таблице п6-п1 значения нет (матрица заполнялась только
выше главной диагонали), но п1-п6 тоже нет,
значит мы смотрим симметричный элемент – п1-п6.
Его значение равно 11 км.
Ответ: 11