Задача 80378 ...
Условие
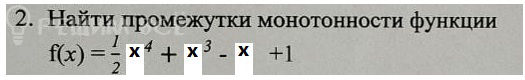
Решение
1. Найдём производную
f′(x)=−2x³+3x²−1.
2. Приравняем её нулю
−2x³+3x²−1=0 ⇔ 2x³−3x²+1=0.
Заметим, что x=1 является корнем: 2−3+1=0.
Разделим многочлен на (x−1):
2x³−3x²+1 = (x−1)(2x²−x−1).
2x²−x−1=0 ⇒ x = 1 или x = −1/2.
Значит
2x³−3x²+1 =(x−1)²(2x+1).
Учтя начальный «минус», получаем
f′(x)=−(x−1)²(2x+1).
Критические точки: x = −1/2 и x = 1
(х = 1 — корень кратности 2).
3. Знак производной
• (−∞,−1/2): 2x+1<0 ⇒ −(…)=+(…) >0 ⇒ f′>0 (возрастает);
• (−1/2,1): 2x+1>0 ⇒ −(…)<0 ⇒ f′<0 (убывает);
• (1,+∞): 2x+1>0, множитель (x−1)²≥0 ⇒ знак остаётся отрицательным, f′<0 (убывает).
В точке x=1 знак не меняется, потому что (x−1)²≥0.
4. Промежутки монотонности
• функция возрастает на (−∞; −1/2);
• функция убывает на (−1/2; +∞).
Дополнительно:
x=−1/2 — точка локального максимума (смена «+» на «−»);
x=1 — стационарная точка без экстремума (f′ меняетcя с «−» на «−», точка перегиба).
Ответ: f(x) возрастает на (−∞; −1/2) и убывает на (−1/2; +∞).