Задача 80362 Найдите все значения параметра a при...
Условие
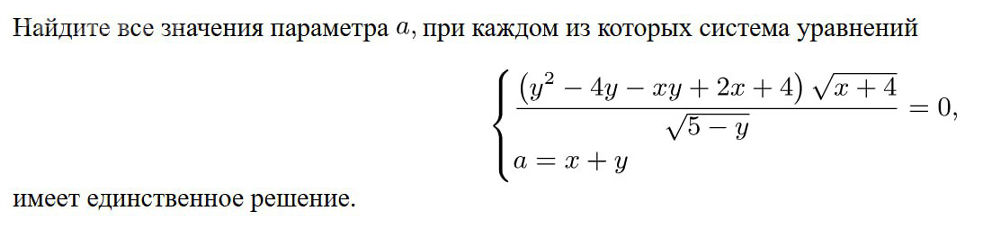
Решение
\frac{(y^2-4y-xy+2x+4) \sqrt{x+4}}{\sqrt{5-y}}=0 \\
a = x + y \\
\end{cases}[/m]
По сути, у нас здесь одно уравнение с двумя неизвестными.
Во втором уравнении просто задается параметр а.
Значит, нужно найти все такие пары (x, y), при которых 1 уравнение имеет решение.
А потом найти все соответствующие а из 2 уравнения.
Решаем 1 уравнение. Область определения функций:
Выражение под корнем должно быть неотрицательным.
Знаменатель дроби не должен равняться 0.
{ x + 4 ≥ 0
{ 5 - y > 0
Получаем:
{ x ≥ -4
{ y < 5
Область определения:
x ∈ [-4; +oo); y ∈ (-oo; 5)
Теперь решаем само уравнение.
(y^2 - 4y - xy + 2x + 4)*sqrt(x + 4) = 0
((y^2 - 4y + 4) - x(y - 2))*sqrt(x + 4) = 0
((y - 2)^2 - x(y - 2))*sqrt(x + 4) = 0
(y - 2)(y - 2 - x)*sqrt(x + 4) = 0
Если произведение равно 0, то один из множителей равен 0.
1) y = 2 ∈ (-oo; 5) - подходит. При этом x ∈ [-4; +oo)
Здесь решений бесконечно много, нам это не подходит.
2) sqrt(x + 4) = 0
x + 4 = 0
x = -4 ∈ [-4; +oo) - подходит. При этом y ∈ (-oo; 5)
Здесь решений бесконечно много, нам это не подходит.
3) y - 2 - x = 0
y = x + 2 - это прямая.
Из области определения получаем:
При x ∈ [-4; +oo) будет y ∈ [-2; +oo). Но y ∈ (-oo; 5). Поэтому
y ∈ [-2; 5), тогда x ∈ [-4; 3). Отсюда из 2 уравнения:
a = x + y ∈ [-6; 8)
Здесь при каждом x будет один y, нам это подходит.
Ответ: a ∈ [-6; 8)
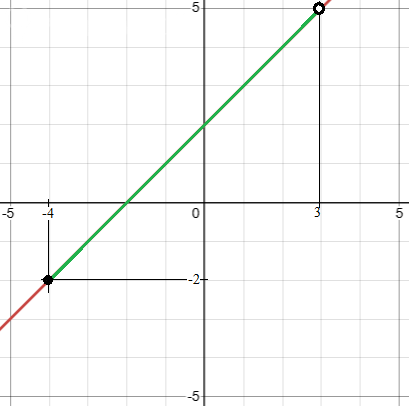
График прилагается.
Нужный отрезок на прямой выделен зеленым цветом.
На концах отмечено, что точка (-4; -2) входит в промежуток, а точка (3; 5) выколота, она в промежуток не входит.