Задача 80359 Как найти площадь пересечения...
Условие
Даны две окружности одинакового единичного радиуса.
Они пересекаются так, как показано на рисунке.
Здесь всё честно - каждая окружность проходит через центр другой окружности.
Как найти площадь их пересечения, выделенную зелёным цветом?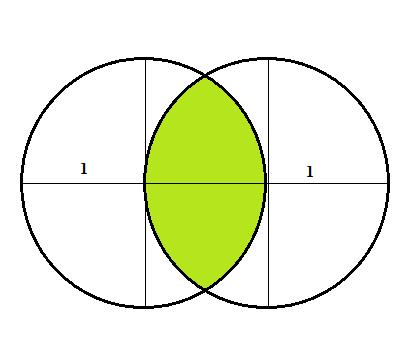
математика 6-7 класс
125
Решение
★
R = 1, d = 1
φ = arccos(d/(2R)) = arccos(1/2) = π/3
θ = 2φ = 2π/3
S_сектор = (1/2)R²θ = π/3
S_тр = (1/2)R² sinθ = (1/2)·1·sin(2π/3) = √3/4
S_сегм = π/3 - √3/4
S = 2·(π/3 - √3/4) = 2π/3 - √3/2
Ответ: 2π/3 - √3/2
