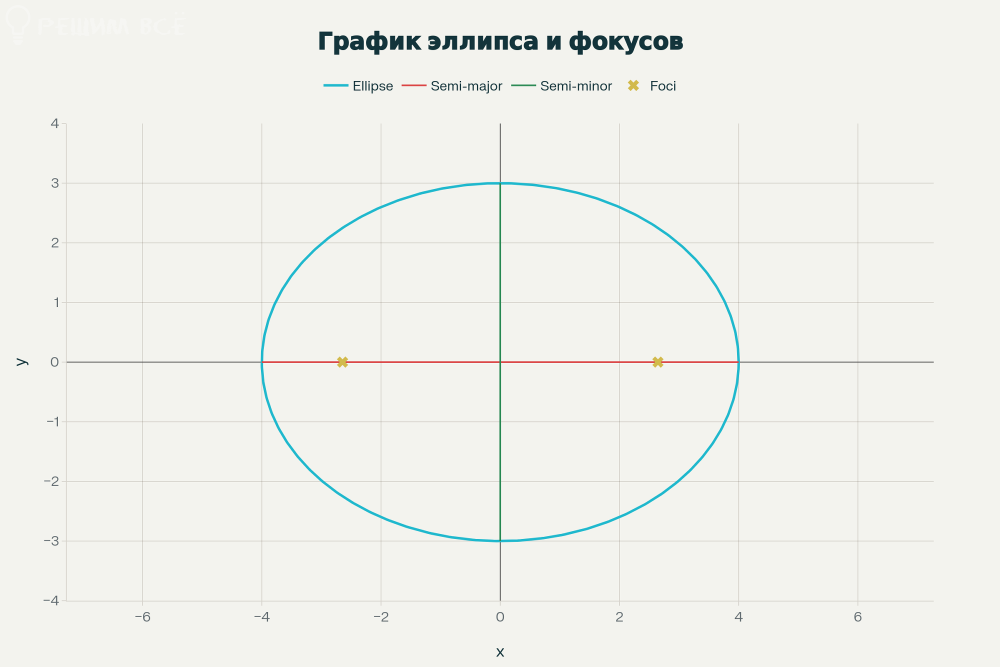
Задача 80349 Определить тип кривой, найти полуоси,...

6791e75b339c2b5e130cfac0

1/23/2025 6:56:22 AM

Определить тип кривой, найти полуоси, фокусы. Нарисовать схематический рисунок. 9x^2+16y^2=144

5f282cfba9074b3a3bc0f013

7/31/2025 5:01:00 PM

★

Дано:
9x^2 + 16y^2 = 144

Решение:

1. Приведем уравнение к каноническому виду:
9x^2 + 16y^2 = 144
x^2/16 + y^2/9 = 1

2. Тип кривой:
Это уравнение эллипса.

3. Полуоси:
a^2 = 16 ⇒ a = 4 (большая полуось)
b^2 = 9 ⇒ b = 3 (малая полуось)

a = 4 — по оси x
b = 3 — по оси y

4. Фокусы:
c = sqrt(a^2 - b^2) = sqrt(16 - 9) = sqrt(7) ≈ 2,65
Координаты фокусов: (±c, 0) ⇒ (±2,65; 0)

Ответ:
Тип: эллипс
Полуоси: a = 4, b = 3
Фокусы: (±2,65; 0)