Задача 80343 26) К двум вертикально расположенным...

66758a5f4a6eb928f58e676d

6/26/2025 11:09:26 AM

26) К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень массой М = 2 кг и длиной L = 40 см. Если к этому стержню подвесить груз на расстоянии d = 5 см от правой пружины, то стержень будет расположен горизонтально, а растяжения обеих пружин будут одинаковы (см. рисунок). Жёсткость левой пружины в 3 раза меньше, чем у правой. Чему равна масса m подвешенного груза? Сделайте рисунок с указанием сил, использованных в решении задачи.
Обоснуйте применимость законов, используемых при решении задачи.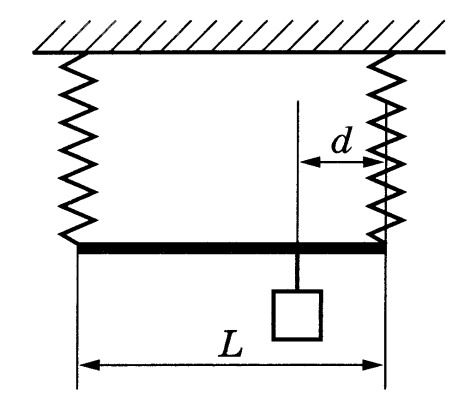

68501b46d00c766c9c688611

6/26/2025 11:10:14 AM

★

Решение

Пусть
• k₁ – жёсткость левой пружины;
• k₂ – жёсткость правой пружины, k₂ = 3k₁;
• x – одинаковое удлинение обеих пружин;
• L = 0,40 м – длина стержня;
• d = 0,05 м – расстояние точки подвеса груза от правой пружины;
• M = 2 кг – масса стержня;
• m – искомая масса груза.

На стержень действуют (см. рисунок):

1. Силы упругости пружин
 F₁ = k₁x (слева, вверх), F₂ = k₂x = 3k₁x (справа, вверх).
2. Вес стержня Mg (вниз, в центре, на расстоянии L/2 от левой пружины).
3. Вес груза mg (вниз, в точке, удалённой на L – d от левой пружины).

I. Условие равновесия по силам
F₁ + F₂ = Mg + mg
k₁x + 3k₁x = (M + m)g ⇒ 4k₁x = (M + m)g. (1)

II. Условие равновесия по моментам относительно левой пружины
(считаем по часовой стрелке положительным)

Mg·(L/2) + mg·(L – d) = F₂·L
Mg·(L/2) + mg·(L – d) = 3k₁x·L. (2)

Подставляем из (1) k₁x = (M + m)g/4:

Mg·(L/2) + mg·(L – d) = 3L·(M + m)g/4.
Сокращая на g и раскрывая скобки, получаем

ML/2 + m(L – d) = 3L(M + m)/4.

Перенеся всё в одну часть и сгруппировав члены при M и m:

–ML/4 + m(L/4 – d) = 0
⇒ m = (ML/4)/(L/4 – d). (3)

III. Числовая подстановка
L/4 = 0,40 м / 4 = 0,10 м.

m = (2 кг · 0,40 м / 4) / (0,10 м – 0,05 м)
 = (0,20 кг·м)/(0,05 м)
 = 4 кг.

Ответ: m = 4 кг.

Обоснование применимости законов

1. Система находится в покое ⇒ выполняются условия статики:
 ΣF = 0 и ΣM = 0.
2. Пружины деформированы в пределах упругости ⇒ справедлив закон Гука F = kx.
3. Стержень считаем абсолютно жёстким, масса распределена равномерно ⇒ его вес приложен в центре.

Следовательно, использованные законы механики применимы.