Задача 80296 1) На рисунке приведён график...
Условие
Ответ: ______________ м/с^2.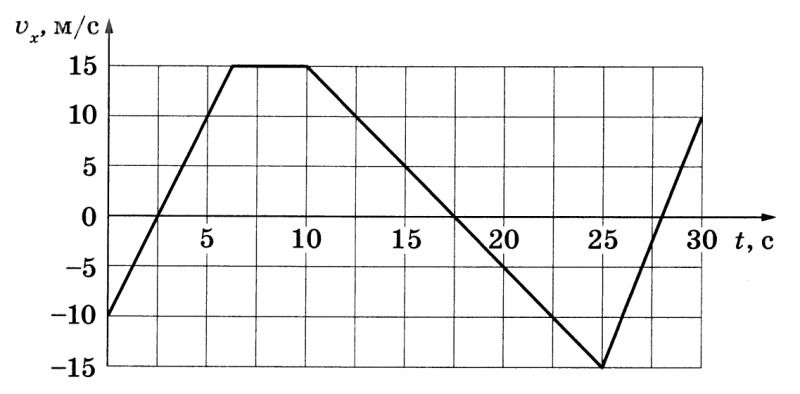
Решение
a_x = Δv_x / Δt, т.е. наклон (угловой коэффициент) участка графика v_x(t).
1. Определим, на каком участке времени находится точка t = 15 с.
Из графика видно, что:
• от 5 до 10 с v_x = 15 м/с (горизонтальный участок, a_x = 0);
• начиная с 10 с скорость линейно убывает от +15 м/с до –15 м/с к 25 с (наклонная прямая).
Следовательно, момент t = 15 с лежит на этом наклонном участке 10–25 с, где ускорение постоянно.
2. Найдём наклон этой прямой:
v_1 = +15 м/с при t_1 = 10 с,
v_2 = –15 м/с при t_2 = 25 с.
a_x = (v_2 – v_1) / (t_2 – t_1)
= (–15 – 15) м/с / (25 – 10) с
= (–30) м/с / 15 с
= –2 м/с².
3. Поскольку ускорение на всём участке 10–25 с постоянно, в любой точке этого интервала, включая t = 15 с, оно равно –2 м/с².
Ответ: –2 м/с².