Задача 79957 вычислить матрицу, задание на картинке...
Условие
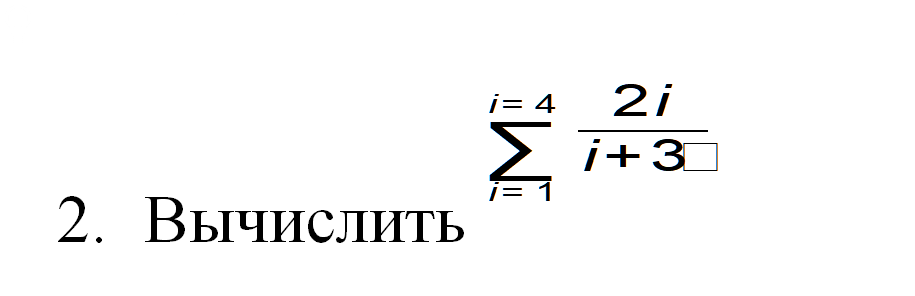
математика ВУЗ
62
Решение
★
то есть 4 слагаемых. Можно их просто посчитать.
Надо сказать, что традиционно сверху пишут только последнее число:
[m]\sum \limits_{i=1}^{4} \frac{2i}{i+3} = \frac{2 \cdot 1}{1+3} + \frac{2 \cdot 2}{2+3} + \frac{2 \cdot 3}{3+3} + \frac{2 \cdot 4}{4+3} =\frac{2}{4} + \frac{4}{5} + \frac{6}{6} + \frac{8}{7} = [/m]
[m]= \frac{1}{2} + \frac{4}{5} + 1 + \frac{8}{7} = \frac{35}{70} + \frac{56}{70} + \frac{70}{70} + \frac{80}{70} = \frac{241}{70} = \frac{210+31}{70}= 3 \frac{31}{70}[/m]