Задача 79955 ...

6826256b2cf64b39fd0bd5c4

5/15/2025 5:35:58 PM

Сторона основания 4 см боковое ребро 10 см. Найти высоту правильной четырëхугольной пирамиду

5f282cfba9074b3a3bc0f013

5/16/2025 8:59:39 AM

★

1. Основание — квадрат со стороной a = 4 см, значит центр основания — точка пересечения диагоналей.
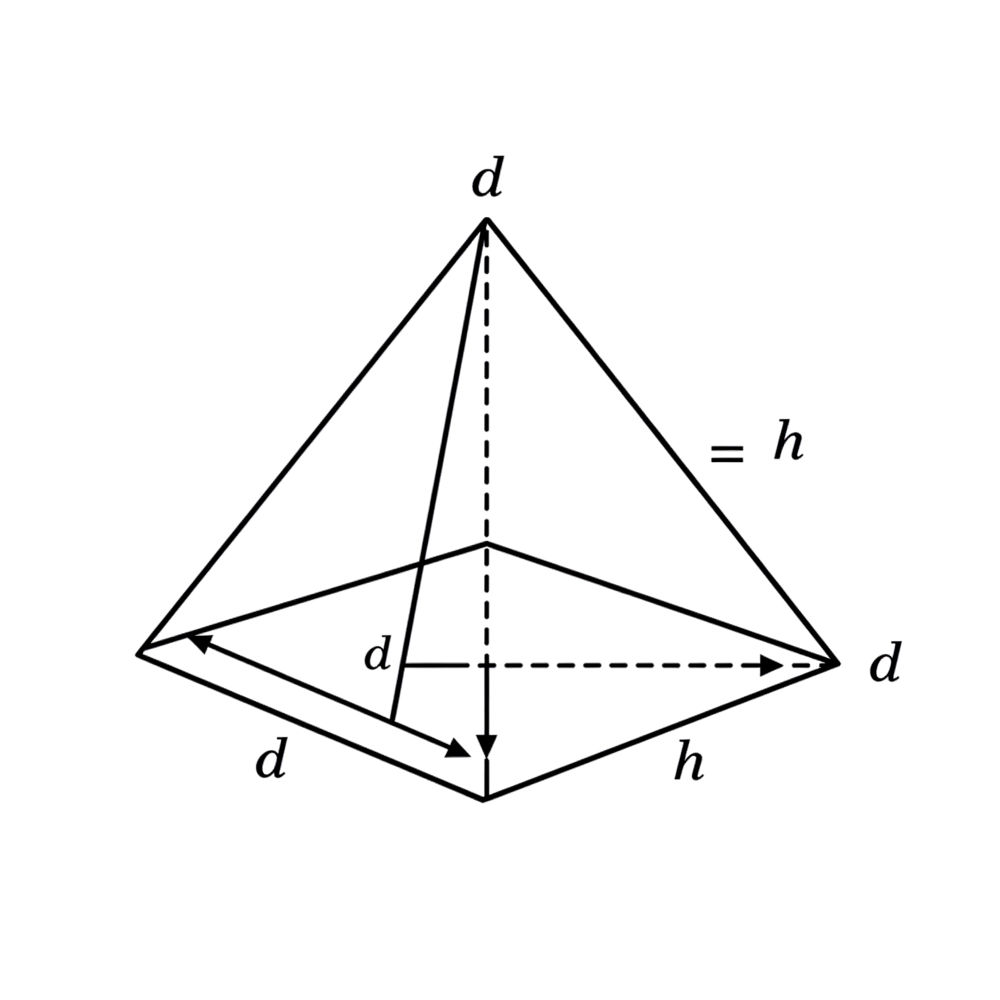
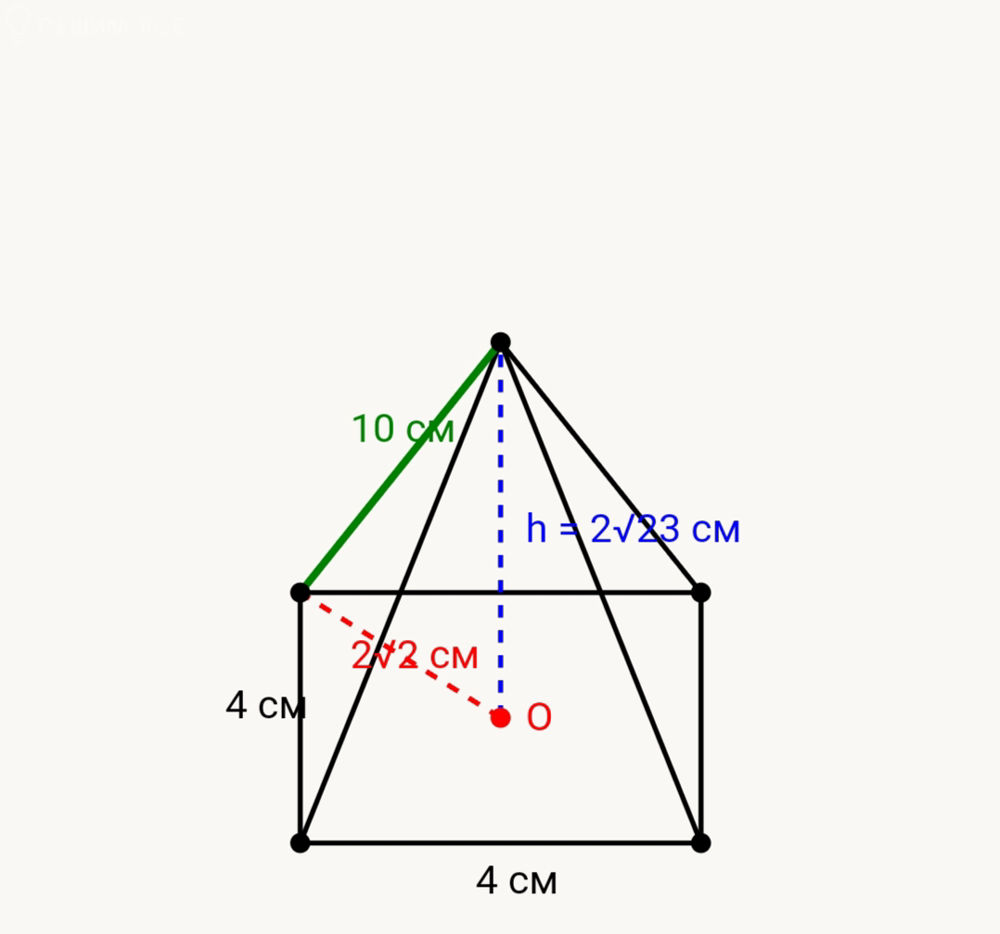
2. Диагональ квадрата [m] d = a\sqrt{2} = 4\sqrt{2} [/m], значит расстояние от центра основания до любой вершины (т.е. половина диагонали) равно:
[m]
r = \frac{d}{2} = \frac{4\sqrt{2}}{2} = 2\sqrt{2}
[/m]
3. Рассмотрим прямоугольный треугольник, в котором:
- гипотенуза — боковое ребро (10 см),
- один катет — искомая высота h,
- другой катет — расстояние от центра основания до вершины основания: [m] 2\sqrt{2} [/m] см.

Применим теорему Пифагора:
[m]
10^2 = h^2 + (2\sqrt{2})^2
[/m]
[m]
100 = h^2 + 4 \cdot 2 = h^2 + 8
[/m]
[m]
h^2 = 92
\Rightarrow h = \sqrt{92} = \sqrt{4 \cdot 23} = 2\sqrt{23}
[/m]

Ответ [m] 2\sqrt{23} [/m]