Задача 79929 Найти решение задачи Коши для системы...
Условие
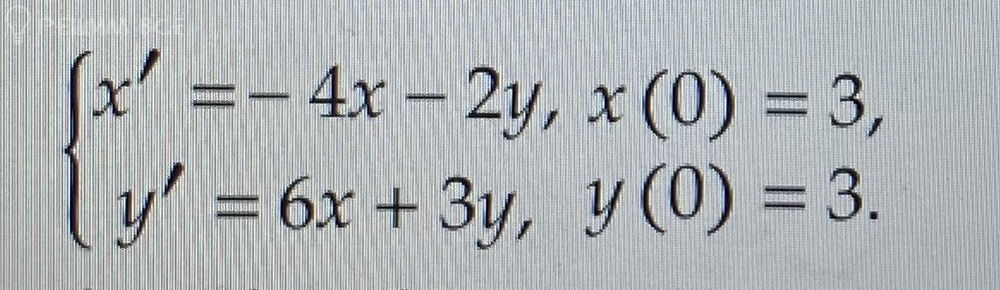
Решение
{ x' = -4x - 2y, x(0) = 3
{ y' = 6x + 3y, y(0) = 3
Здесь важно понимать, что x(t) и y(t) - это функции от третьей переменной t, которой в системе нет, но она предполагается. Решением будет система функций:
{ x(t) = ...
{ y(t) = ...
Чтобы решить систему, нужно из 2 уравнения выразить x:
6x = y' - 3y
x = y'/6 - y/2
Обычно вместо x', y' записывают dx/dt, dy/dt, и коэффициенты выносят вперед:
[m]\large x(t) = \frac{1}{6} \cdot \frac{dy}{dt} - \frac{1}{2} \cdot y[/m]
Находим производную этой функции:
[m]\large \frac{dx}{dt} = \frac{1}{6} \cdot \frac{d^2y}{dt^2} - \frac{1}{2} \cdot \frac{dy}{dt}[/m]
И подставляем всё это в первое уравнение:
[m]\large \frac{1}{6} \cdot \frac{d^2y}{dt^2} - \frac{1}{2} \cdot \frac{dy}{dt} = -4(\frac{1}{6} \cdot \frac{dy}{dt} - \frac{1}{2} \cdot y) - 2y[/m]
Раскрываем скобки и приводим подобные:
[m]\large \frac{1}{6} \cdot \frac{d^2y}{dt^2} - \frac{1}{2} \cdot \frac{dy}{dt} = -\frac{4}{6} \cdot \frac{dy}{dt} +2y - 2y[/m]
[m]\large \frac{1}{6} \cdot \frac{d^2y}{dt^2} - \frac{1}{2} \cdot \frac{dy}{dt} + \frac{2}{3} \cdot \frac{dy}{dt} = 0[/m]
Умножаем всё на 6:
[m]\large \frac{d^2y}{dt^2} - 3 \cdot \frac{dy}{dt} + 4 \cdot \frac{dy}{dt} = 0[/m]
[m]\large \frac{d^2y}{dt^2} + \frac{dy}{dt} = 0[/m]
Получили совсем простое линейное уравнение 2 порядка.
Характеристическое уравнение:
k^2 + k = 0
k1 = 0; k2 = -1
[m]\large y(t) = C1 e^{0t} + C2 e^{-1t}[/m]
[m]\large y(t) = C1 + C2 e^{-t}[/m]
[m]\large \frac{dy}{dt} = -C2 e^{-t}[/m]
Подставляем это в выражение для x(t):
[m]\large x(t) = \frac{1}{6} \cdot \frac{dy}{dt} - \frac{1}{2} \cdot y[/m]
[m]\large x(t) = \frac{1}{6} \cdot (-C2 e^{-t}) - \frac{1}{2} \cdot (C1 + C2 e^{-t})[/m]
[m]\large x(t) = -\frac{C2}{6} \cdot e^{-t} - \frac{C1}{2} - \frac{C2}{2} e^{-t}[/m]
[m]\large x(t) = -\frac{2 \cdot C2}{3} \cdot e^{-t} - \frac{C1}{2}[/m]
Решение системы диф. уравнений:
[b]{ [m]\large x(t) = - \frac{C1}{2} - \frac{2 \cdot C2}{3} \cdot e^{-t}[/m]
{ [m]\large y(t) = C1 + C2 e^{-t}[/m][/b]
Теперь решаем задачу Коши:
{ x(0) = 3
{ y(0) = 3
Находим x(0) и y(0):
{ [m]\large x(0) = - \frac{C1}{2} - \frac{2 \cdot C2}{3} \cdot e^{0} = - \frac{C1}{2} - \frac{2 \cdot C2}{3}[/m]
{ [m]\large y(0) = C1 + C2 e^{0} = C1 + C2[/m]
Подставляем:
{ [m]- \frac{C1}{2} - \frac{2 \cdot C2}{3} = 3[/m]
{ [m]C1 + C2 = 3[/m]
Получили систему линейных уравнений, решаем ее подстановкой:
{ [m]C2 = 3 - C1[/m]
{ [m]- \frac{C1}{2} - \frac{2 \cdot (3 - C1)}{3} = 3[/m]
Умножаем 2 уравнение на 6:
-3*C1 - 4*(3 - C1) = 3
-3*C1 - 12 + 4*C1 = 3
C1 = 15
C2 = 3 - C1 = 3 - 15 = -12
Коэффициенты нашли, теперь записываем функции с этими коэффициентами:
{ [m]\large x(t) = - \frac{15}{2} - \frac{2 \cdot (-12)}{3} \cdot e^{-t}[/m]
{ [m]\large y(t) = 15 - 12 e^{-t}[/m]
Решение задачи Коши:
[b]{ [m]\large x(t) = - 7,5 + 8e^{-t}[/m]
{ [m]\large y(t) = 15 - 12 e^{-t}[/m][/b]