Задача 79926 ...
Условие
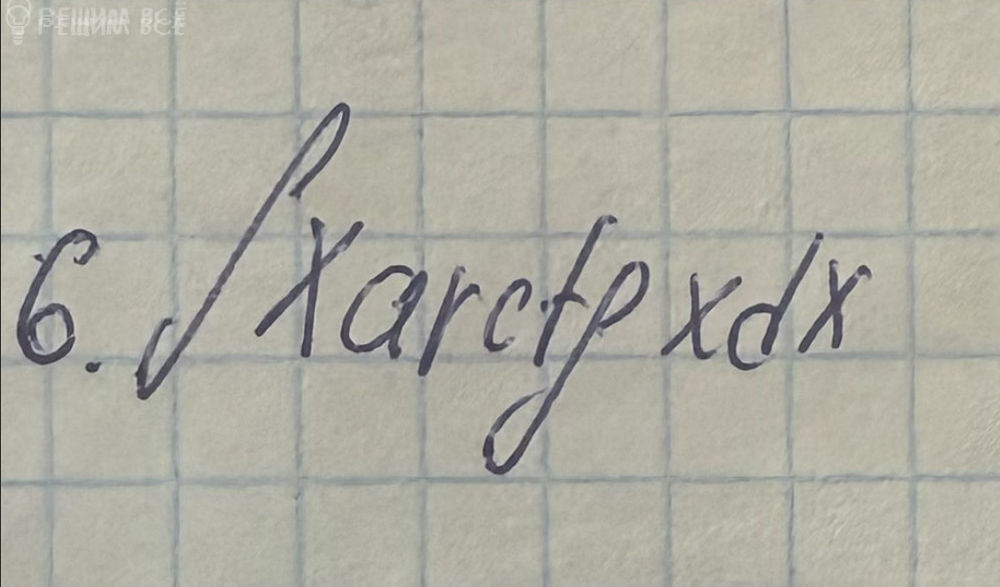
математика ВУЗ
93
Решение
★
u = arctg(x), тогда du = dx / (1 + x²),
dv = x dx, тогда v = x² / 2.
Тогда по формуле интегрирования по частям
∫u dv = uv − ∫v du
получаем:
∫ x·arctg(x) dx = (x²/2)·arctg(x) − ∫(x²/2)·(1/(1 + x²)) dx.
Далее упростим второй интеграл:
∫ (x²/(1 + x²)) dx = ∫ [1 − (1/(1 + x²))] dx = ∫ 1 dx − ∫ (1/(1 + x²)) dx = x − arctg(x).
Таким образом,
∫ x·arctg(x) dx = (x²/2)·arctg(x) − (1/2)[x − arctg(x)] + C,
что можно записать в развёрнутом виде как
∫ x·arctg(x) dx = [b](x²/2)·arctg(x) − x/2 + (1/2)·arctg(x) + C[/b].