Задача 79921 Найдите математическое ожидание М(Х),...
Условие
1 вариант 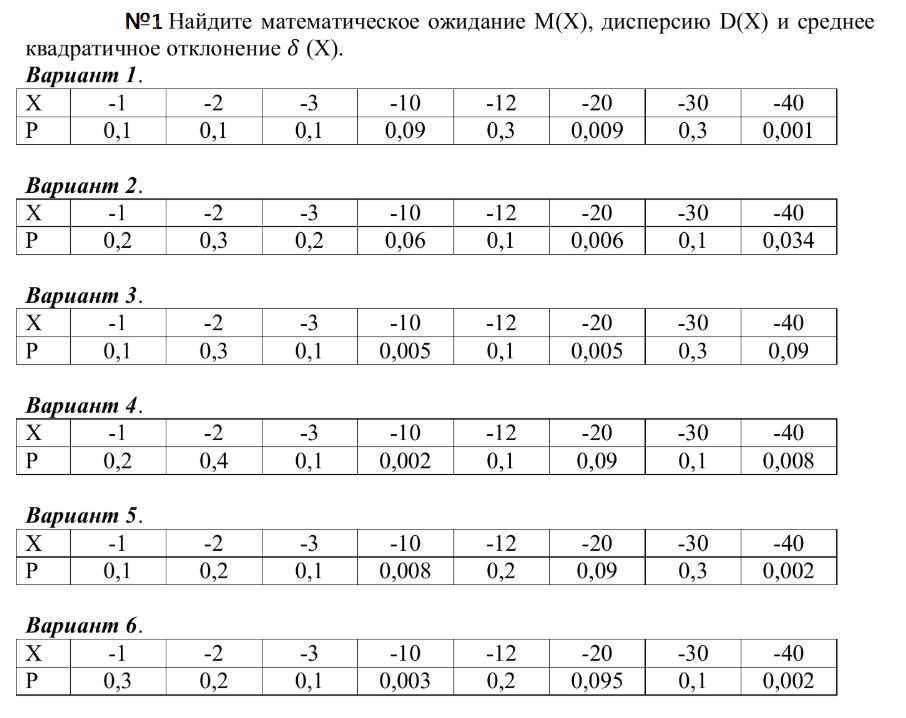
Решение
1) Сначала вычислим математическое ожидание
M(X)=∑(xᵢ pᵢ).
Подставляя данные из таблицы:
• (–1)·0,1 = –0,1
• (–2)·0,1 = –0,2
• (–3)·0,1 = –0,3
• (–10)·0,09 = –0,9
• (–12)·0,3 = –3,6
• (–20)·0,009 = –0,18
• (–30)·0,3 = –9
• (–40)·0,001 = –0,04
Суммируем все слагаемые:
M(X)=–0,1 + (–0,2)+ (–0,3)+ (–0,9)+ (–3,6)+ (–0,18)+ (–9)+ (–0,04)=–14,32.
2) Далее найдём E(X²)=∑(xᵢ² pᵢ), где xᵢ² – квадрат значения признака.
• (–1)²·0,1 = 1·0,1 = 0,1
• (–2)²·0,1 = 4·0,1 = 0,4
• (–3)²·0,1 = 9·0,1 = 0,9
• (–10)²·0,09 = 100·0,09 = 9
• (–12)²·0,3 = 144·0,3 = 43,2
• (–20)²·0,009 = 400·0,009 = 3,6
• (–30)²·0,3 = 900·0,3 = 270
• (–40)²·0,001 = 1600·0,001 = 1,6
Складываем:
E(X²)=0,1+0,4+0,9+9+43,2+3,6+270+1,6=328,8.
3) Дисперсия D(X) равна
D(X)=E(X²)–[M(X)]²=328,8–(–14,32)².
(–14,32)² ≈ 205,06, откуда
D(X)=328,8–205,06=123,74 (примерно).
4) Среднее квадратичное отклонение
σ(X)=√D(X) ≈ √123,74 ≈ 11,12.
Ответ (округляя до двух знаков после запятой):
• M(X)=–14,32,
• D(X)=123,74,
• σ(X)=11,12.