Задача 79920 ...
Условие
8. ∫[от -π/3 до π/4] 2tgx dx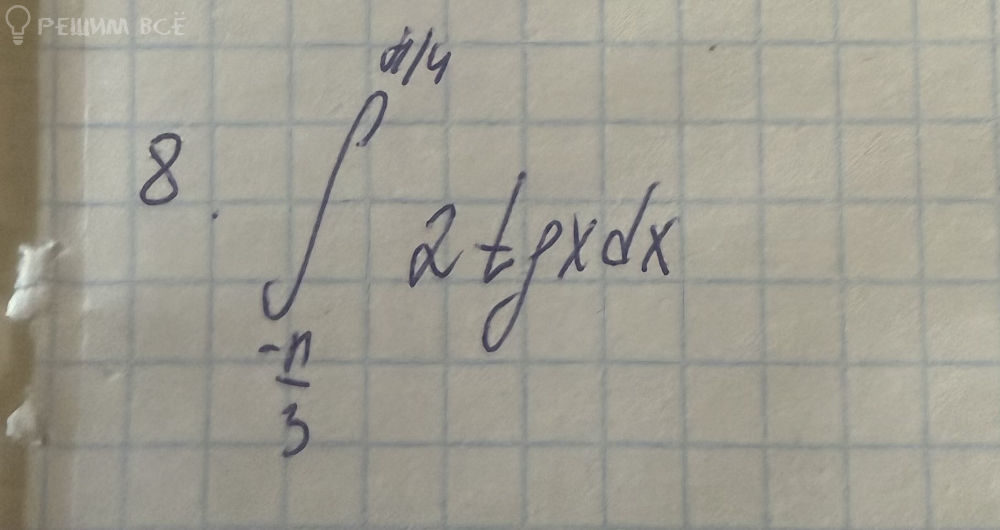
математика ВУЗ
55
Решение
★
Замена cos x = t, dt = -sin x dx, t(-π/3) = cos(-π/3) = 1/2; t(π/4) = cos π/4 = sqrt(2)/2
[m]2 \int \limits_{-\pi/3}^{\pi/4} \frac{\sin x}{\cos x} dx = -2 \int \limits_{1/2}^{\sqrt{2}/2} \frac{dt}{t} = -2 \ln |t| \bigg |_{1/2}^{\sqrt{2}/2} = -2 (\ln |\frac{\sqrt{2}}{2}| - \ln |\frac{1}{2}|) =[/m]
[m]= -2(\ln \sqrt{2} - \ln 2 + \ln 2) = -2 \ln \sqrt{2} = -2 \cdot 0,5 \ln 2 = -\ln 2[/m]