Задача 79890 Вычислить интеграл от рациональной...
Условие
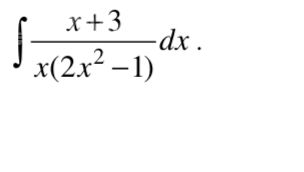
Решение

Все решения
Применяем метод неопределенных коэффициентов.
Можно было бы разложить разность квадратов:
[m]x^2 - \frac{1}{2} = (x - \frac{1}{\sqrt{2}})(x + \frac{1}{\sqrt{2}})[/m]
Но мы не будем связываться с корнями из 2, поэтому напишем так:
[m]\frac{x+3}{x(x^2-1/2)} = \frac{Ax+B}{x^2-1/2} + \frac{C}{x} = \frac{x(Ax+B) + C(x^2 - 1/2)}{x(x^2-1/2)} = \frac{x^2(A + C) + Bx - C/2}{x(x^2-1/2)}[/m]
Составляем систему:
{ A + C = 0
{ B = 1
{ -C/2 = 3
Решаем:
{ C = -6
{ B = 1
{ A = -C = 6
Получаем интеграл:
[m]\frac{1}{2} \cdot \bigg( \int \frac{6x+1}{x^2-1/2} dx + \int \frac{-6}{x} dx \bigg) = \frac{1}{2} \cdot \bigg( 6 \int (-\frac{xdx}{1/2 - x^2}) - \int \frac{dx}{1/2 - x^2} - 6\int \frac{dx}{x} \bigg)[/m]
Есть табличные интегралы:
[m]\int \frac{xdx}{a^2 - x^2} = -\frac{1}{2} \ln \bigg| a^2 - x^2\bigg|[/m]
[m]\int \frac{dx}{a^2 - x^2} = \frac{1}{2a} \ln \bigg| a^2 - x^2\bigg|[/m]
[m]\int \frac{dx}{x} = \ln |x|[/m]
В нашем случае:
[m]\int \frac{xdx}{1/2 - x^2} = -\frac{1}{2} \ln \bigg|\frac{1}{2} - x^2\bigg|[/m]
[m]\int \frac{dx}{1/2 - x^2} = \frac{1}{2 \cdot 1/\sqrt{2}} \ln \bigg| \frac{1/\sqrt{2} + x}{1/\sqrt{2} - x}\bigg|[/m]
Получаем:
[m]\frac{1}{2} \cdot \bigg( 6 \int (-\frac{xdx}{1/2 - x^2}) - \int \frac{dx}{1/2 - x^2} - 6\int \frac{dx}{x} \bigg) = [/m]
[m] = \frac{1}{2} \cdot \bigg( 6 \cdot \frac{1}{2} \ln \bigg|\frac{1}{2} - x^2\bigg| - \frac{1}{2 \cdot 1/\sqrt{2}} \ln \bigg| \frac{1/\sqrt{2} + x}{1/\sqrt{2} - x}\bigg| - 6 \ln |x| \bigg) +C =[/m]
[m]= \frac{3}{2} \ln \bigg|\frac{1}{2} - x^2\bigg| - \frac{\sqrt{2}}{4} \ln \bigg| \frac{1/\sqrt{2} + x}{1/\sqrt{2} - x}\bigg| - 3 \ln |x| + C[/m]