Задача 79876 Выполните задания с дано, решение и...

66165ea3e9af3b6296a21bb6

5/10/2025 7:24:08 AM

Выполните задания с дано, решение и рисунок: 2. Найдите длину диагонали прямоугольного параллелепипеда, измерения которого равны 6 см, 8 см, и 10 см.

626fab9a354ab65fb2f43abb

5/11/2025 11:04:58 AM

★

Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед.
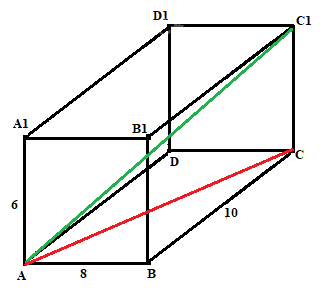
AB = 8 см, BC = 10 см, AA1 = 6 см
Найти: AC1

Решение. Диагональ AC1 на рисунке показана зеленым цветом.
Нарисуем дополнительно диагональ основания AC. Она показана красным.
Из прямоуголного треугольника ABC по теореме Пифагора:
AC^2 = AB^2 + BC^2 = 8^2 = 10^2 = 64 + 100 = 164
Мы не будем извлекать корень, потому что нам нужен квадрат этой диагонали.
Из прямоуголного треугольника ACC1 по теореме Пифагора:
AC1^2 = AC^2 + CC1^2 = 164 + 6^2 = 164 + 36 = 200
AC1 = sqrt(200) = 10*sqrt(2)

В итоге получается: чтобы найти диагональ параллелепипеда,
надо сложить квадраты всех его сторон и извлечь квадратный корень:
AC1 = sqrt(AB^2 + BC^2 + AA1^2) = sqrt(8^2 + 10^2 + 6^2) = sqrt(200) = 10*sqrt(2)

Ответ: 10*sqrt(2)