Задача 79869 непрерывная случайная величина Х задана...
Условие
построить график функции распределения F(x)
найти функцию плотности f(x) и построить ее график
найти математическое ожидание, дисперсию и среднее квадратическое отклонение непрерывной случайной величины Х
Решение
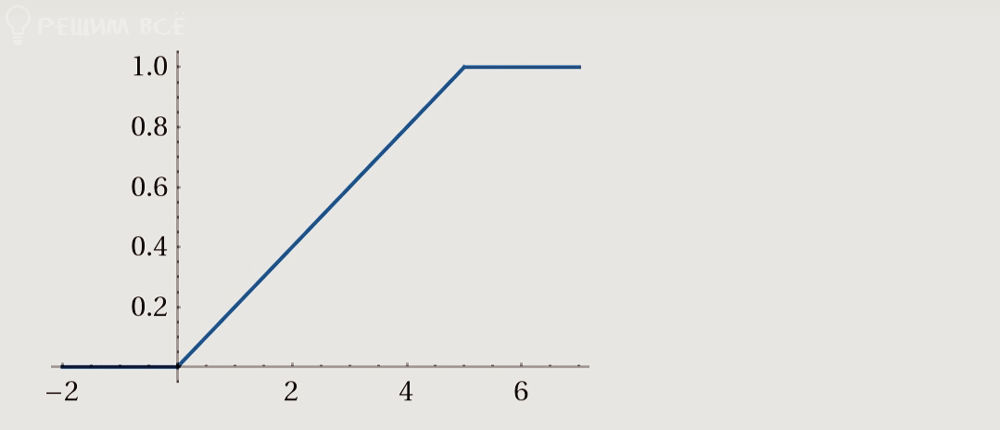
1) График функции распределения F(x)
По условию,
• F(x) = 0 при x ≤ 0,
• F(x) = x/5 при 0 < x ≤ 5,
• F(x) = 1 при x > 5.
Графически это означает:
– при x ≤ 0 функция равна 0 (горизонтальный отрезок);
– на отрезке (0,5) функция линейно возрастает от 0 до 1;
– при x > 5 функция равна 1 (горизонтальный отрезок).
2) Функция плотности f(x)
Плотность есть производная от F(x) по x (там, где F(x) дифференцируема). Из линейного участка F(x) = x/5 на (0,5) получаем
f(x) = 1/5 при 0 < x < 5
и f(x) = 0 при всех остальных x.
3) Математическое ожидание M(X)
Поскольку на (0,5) плотность постоянна 1/5, это распределение равномерно на [0,5].
Формула для математического ожидания равномерного распределения на [0,5]:
M(X) = (0 + 5)/2 = 2.5.
4) Дисперсия D(X)
Для равномерного распределения на [0,5] дисперсия равна
D(X) = (5 – 0)² / 12 = 25/12.
5) Среднее квадратическое отклонение σ(X)
Это корень из дисперсии:
σ(X) = √(25/12) = 5 / √12 ≈ 1.44.
Итоговые ответы:
• F(x): 0 при x ≤ 0; x/5 при 0 < x ≤ 5; 1 при x > 5.
• f(x): 0 при x < 0; 1/5 при 0 < x < 5; 0 при x > 5.
• M(X) = 2.5.
• D(X) = 25/12.
• σ(X) = 5 / √12 ≈ 1.44.
Все решения
F(x) = { 0, x ≤ 0
{ x/5, 0 < x ≤ 5
{ 1, x > 5
2. Функция плотности (производная от F(x)):
f(x) = { 0, x ≤ 0
{ 1/5, 0 < x < 5
{ 0, x ≥ 5
3. Математическое ожидание:
E(X) = ∫[0,5] x*(1/5) dx
= (1/5)*[x²/2]₀⁵
= (1/5)*(25/2)
= 2.5
4. Второй момент:
E(X²) = ∫[0,5] x²*(1/5) dx
= (1/5)*[x³/3]₀⁵
= (1/5)*(125/3)
= 25/3 ≈ 8.333
5. Дисперсия:
D(X) = E(X²) - [E(X)]²
= 25/3 - (5/2)²
= 25/3 - 25/4
= (100-75)/12
= 25/12 ≈ 2.083
6. Среднеквадратичное отклонение:
σ(X) = √D(X)
= √(25/12)
= 5/(2√3)
= (5√3)/6 ≈ 1.443