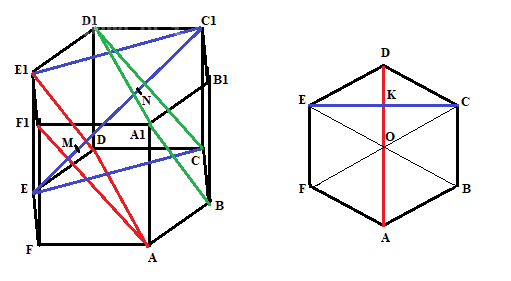
Задача 79799 В правильной шестиугольной призме...

680a854824fa9b4da5cf2445

4/24/2025 7:38:51 PM

В правильной шестиугольной призме найдите расстояние от E до плоскости ADE1. Если сторона основания AB =2 корня из 6, AA1 = 3 корня из 2. Покажите с рисунком пожалуйста

626fab9a354ab65fb2f43abb

4/24/2025 9:29:21 PM

★

Дано: 6-угольная правильная призма
Сторона основания: AB = 2sqrt(6)
Высота AA1 = 3sqrt(2)
Найти расстояние от вершины E до плоскости ADE1.

Смотрите рисунок.
Плоскость (ADE1) дает сечение ADE1F1. Оно показано красным.
Рядом для наглядности показан 6-угольник в основании ABCDEF.
Проводим в нем красную диагональ AD, и перпендикуляр к ней из т. E.
Это оказалась синяя диагональ EC. Находим центр 6-угольника O.
Получаем точку K в пересечении AD с EC.

Как известно, у 6-угольника сторона равна радиусу описанной окружности:
EF = DE = OD = OE. Поэтому ΔODE - равносторонний.
Высота этого треугольника EK = DE*sqrt(3)/2 = 2sqrt(6)*sqrt(3)/2 = 3sqrt(2)
Тогда диагональ EC = 2*EK = 6sqrt(2)

Рассмотрим сечение ECC1E1.
Это прямоугольник со сторонами EC = 6sqrt(2) и CC1 = 3sqrt(2).
Его диагональ EC1 = sqrt(EC^2 + CC1^2) = sqrt((6sqrt(2))^2 + (3sqrt(2))^2) = sqrt(36*2 + 9*2) = sqrt(90) = 3sqrt(10)

Если нарисовать дополнительно сечение A1BCD1, показанное на призме зеленым,
то становится ясно, что плоскости сечений параллельны:
(ADE1F1) || (A1BCD1)
И также ясно, что эти две плоскости делят диагональ EC1 на 3 равные части в силу симметрии призмы.
Точки M и N пересечения диагонали с плоскостями также показаны.
Поэтому расстояние от точки E до плоскости (ADE1) равно:
|E; (ADE1)| = |EM| = EC1/3 = 3sqrt(10)/3 = sqrt(10)

Ответ: sqrt(10)