Задача 79745 ...
Условие
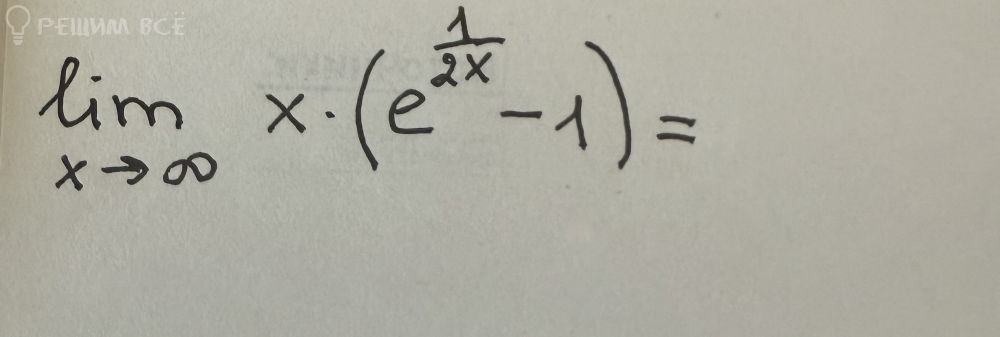
Решение
Сначала сделаем из произведения дробь.
[m]\large \lim \limits_{x \to \infty} x \cdot (e^{\frac{1}{2x}} - 1) = \lim \limits_{x \to \infty} \frac{e^{\frac{1}{2x}} - 1}{\frac{1}{x}} = \frac{e^{\frac{1}{\infty}} - 1}{\frac{1}{\infty}} = \frac{e^0 - 1}{0} = \frac{0}{0}[/m]
Применяем правило Лопиталя – берем производные от числителя и от знаменателя.
[m]\large \lim \limits_{x \to \infty} \frac{e^{\frac{1}{2x}} \cdot (-\frac{1}{2x^2})}{-\frac{1}{x^2}} = \lim \limits_{x \to \infty} \frac{e^{\frac{1}{2x}}}{2} = \frac{e^{\frac{1}{\infty}}}{2} = \frac{e^0}{2} = \frac{1}{2} = 0,5[/m]