Задача 79738 ...
Условие
б) Найдите все корни этого уравнения, принадлежащие отрезку [ -4π ; -5π/2 ].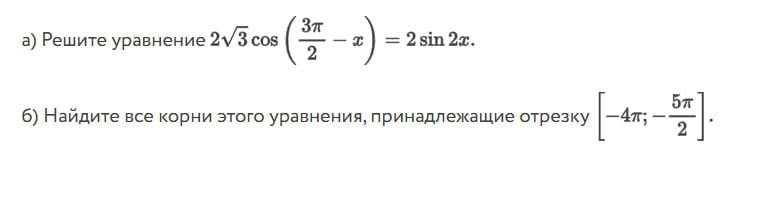
Решение
[m]2 \sqrt{3} \cos (\frac{3 \pi}{2} - x) = 2 \sin 2x[/m]
Во-первых, можно обе части разделить на 2:
[m]\sqrt{3} \cos (\frac{3 \pi}{2} - x) = \sin 2x[/m]
Во-вторых, воспользуемся формулами из тригонометрии:
[m]\cos (\frac{3 \pi}{2} - x) = - \sin x[/m]
[m]\sin 2x = 2 \sin x \cos x[/m]
Подставляем:
[m]-\sqrt{3} \sin x = 2 \sin x \cos x[/m]
Переносим все направо:
[m]0 = 2 \sin x \cos x + \sqrt{3} \sin x[/m]
Выносим sin x за скобки:
[m]\sin x (2 \cos x + \sqrt{3}) = 0[/m]
Если произведение равно 0, то один из множителей равен 0.
1) sin x = 0
x1 = π*k, k ∈ Z
2) 2cos x + sqrt(3) = 0
cos x = -sqrt(3)/2
x2 = ± 5π/6 + 2π*n, n ∈ Z
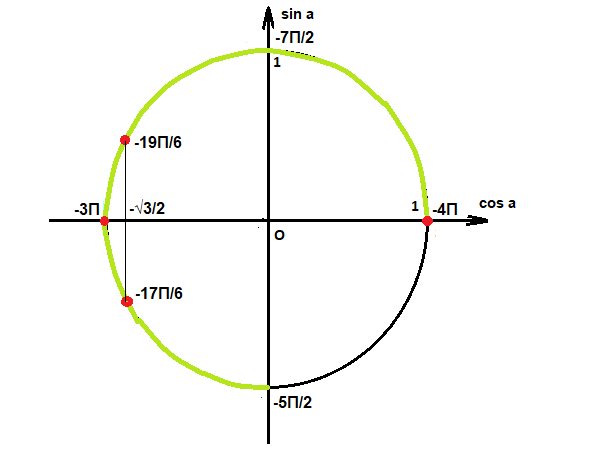
б) Найти корни, принадлежащие отрезку [-4π; -5π/2]
Корни из 1 варианта: x1 = -4π; x2 = -3π
Корни из 2 варианта: x3 = 5π/6 - 4π = -19π/6; x4 = - 5π/6 - 2π = -17π/6
На рисунке промежуток [-4π; -5π/2] показан зеленым цветом.
Решения показаны красными точками.
Ответ: а) x1 = π*k, k ∈ Z; x2 = ± 5π/6 + 2π*n, n ∈ Z
б) x1 = -4π; x2 = -3π; x3 = -19π/6; x4 = -17π/6