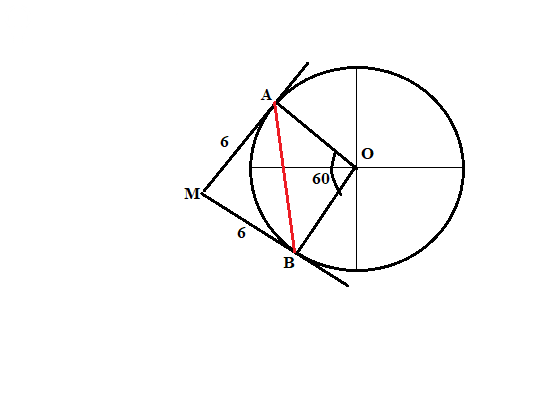
Задача 79680 Из точки М к окружности с центром О...

67f0e2b07794c30488a71f0e

4/5/2025 8:00:18 AM

Из точки М к окружности с центром О проведены касательные МА и МВ. Найдите расстояние между точками касания, если угол АОВ = 60° MA = MB = 6.

626fab9a354ab65fb2f43abb

4/5/2025 9:01:26 AM

★

Смотрите рисунок.
Радиусы OA и OB перпендикулярны касательным MA и MB.
Сумма углов 4-угольника MAOB равна 360°
Значит, AMB = 360° - 90° - 90° - 60° = 120°
Расстояние AB между точками касания можно найти по теореме косинусов:
AB^2 = MA^2 + MB^2 - 2*MA*MB*cos AMB
AB^2 = 6^2 + 6^2 - 2*6*6*cos 120° = 36 + 36 - 2*36*(-1/2) = 72 + 36 = 108
AB = sqrt(108) = sqrt(3*36) = 6sqrt(3)