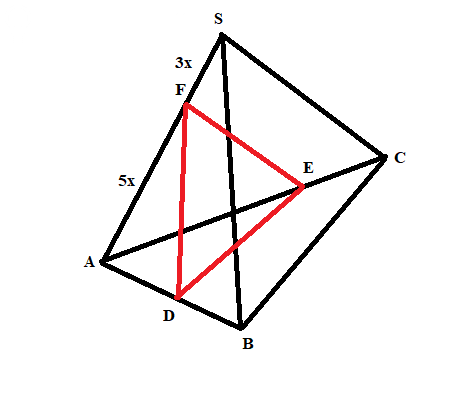
Задача 79678 В правильной треугольной пирамиде SABC...

67efaeb57794c30488a71ce1

4/4/2025 9:38:57 PM

В правильной треугольной пирамиде SABC проведено сечение, параллельное грани SCB, которое делит ребро SA в отношении 3 : 5, считая от вершины S. Найдите объём пирамиды SABC, если расстояние от точки A до плоскости сечения – 1,25, а площадь сечения – 15.

626fab9a354ab65fb2f43abb

4/5/2025 1:18:05 PM

★

Я написал ответ, но он сорвался и пропал.
У меня уже нет желания писать его снова.
Решение основано на том, что нужно вычислить объем пирамиды
с вершиной в А и основанием - плоскостью сечения DEF.
Расстояние от вершины А до плоскости сечения - это высота h(A; DEF) = 1,25
Площадь сечения нам дана: S(DEF) = 15
V(ADEF) = 1/3*h(A; DEF)*S(DEF) = 1/3*1,25*15 = 6,25
Объем нашей пирамиды SABC будет в 8^3/5^3 = 512/125 раз больше, чем объем этой пирамиды с сечением ADEF.
Могу дать рисунок и готовый ответ.
Ответ: V(SABC) = 512/125*6,25 = 25,6