Задача 78974 8. Даны координаты вершин пирамиды...
Условие
9. Составить каноническое уравнение прямой:
[m]
\begin{cases}
2x + 3y - 2z = 5 = 0, \\
x + y + 3z + 6 = 0.
\end{cases}
[/m]
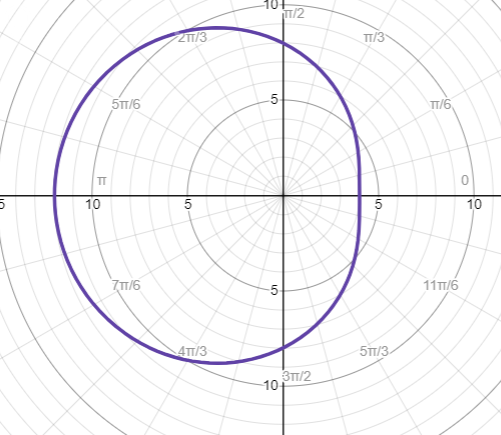
10. Построить кривую $p = 4(2 - \cos \varphi)$, заданную в полярных координатах.
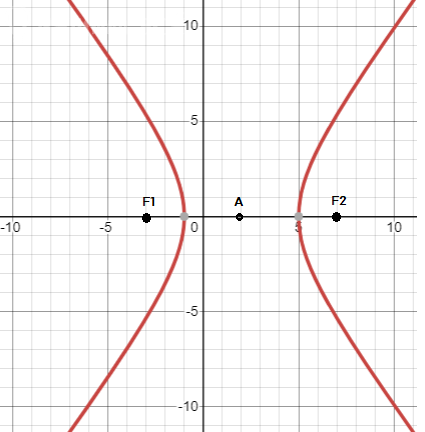
11. Вывести уравнение кривой, если абсолютная величина разности расстояний от каждой ее точки до точек $F_1(-3; 0)$ и $F_2(7; 0)$ есть величина постоянная и равна $p = 6$. Сделать чертеж.
12. Привести уравнение $36x^2 + 49y^2 + 72x - 196y - 1442 = 0$ к каноническому виду, определить тип кривой и сделать чертеж.
Решение
{ 2x + 3y - 2z - 5 = 0
{ x - y + 3z + 6 = 0
Принимаем, например, z = 1 и решаем систему:
{ x - y - 2 + 6 = 0
{ 2x + 3y + 3 - 5 = 0
Приводим подобные:
{ x - y + 4 = 0
{ 2x + 3y - 2 = 0
Умножаем 1 уравнение на 3:
{ 3x - 3y + 12 = 0
{ 2x + 3y - 2 = 0
Складываем уравнения:
5x + 0y + 10 = 0
5x = -10
x = -10/5 = -2
Из 1 уравнения:
y = x + 4
y = 2
Нашли одну точку A(-2; 2; 1)
Принимаем, например, z = -4 и решаем систему:
{ x - y + 8 + 6 = 0
{ 2x + 3y - 12 - 5 = 0
Приводим подобные:
{ x - y + 14 = 0
{ 2x + 3y - 17 = 0
Умножаем 1 уравнение на 3:
{ 3x - 3y + 42 = 0
{ 2x + 3y - 17 = 0
Складываем уравнения:
5x + 0y + 25 = 0
5x = -25
x = -25/5 = -5
Из 1 уравнения:
y = x + 14
y = 9
Нашли вторую точку B(-5; 9; -4)
Составляем уравнение прямой по двум точкам:
A(-2; 2; 1) и B(-5; 9; -4)
[m]\frac{x + 5}{-2 + 5} = \frac{y - 9}{2 - 9} = \frac{z + 4}{1 + 4}[/m]
Ответ:
[m](AB):\ \ \large \frac{x + 5}{3} = \frac{y - 9}{-7} = \frac{z + 4}{5}[/m]
10. Построить кривую:
p = 4(2 - cos φ )
Чертеж я построил, смотрите рисунок 1.
Но это на специальном сайте.
Как это делается вручную, я не знаю.
11. F1(-3; 0); F2(7; 0)
Разность расстояний от любой точки кривой M(x; y) равна p = 6.
[m]|MF1| = \sqrt{(x + 3)^2 + (y - 0)^2} = \sqrt{(x + 3)^2 + y^2}[/m]
[m]|MF2| = \sqrt{(x - 7)^2 + (y - 0)^2} = \sqrt{(x - 7)^2 + y^2}[/m]
Разность расстояний:
[m]|MF2| - |MF1| = \sqrt{(x - 7)^2 + y^2} - \sqrt{(x + 3)^2 + y^2} = 6[/m]
Разделяем корни:
[m]\sqrt{(x - 7)^2 + y^2} = 6 + \sqrt{(x + 3)^2 + y^2}[/m]
Возводим в квадрат обе части:
[m](x - 7)^2 + y^2 = (6 + \sqrt{(x + 3)^2 + y^2})^2[/m]
[m](x - 7)^2 + y^2 = 36 + 12\sqrt{(x + 3)^2 + y^2} + (x + 3)^2 + y^2[/m]
[m]x^2 - 14x + 49 + y^2 = 36 + 12\sqrt{(x + 3)^2 + y^2} + x^2 + 6x + 9 + y^2[/m]
Приводим подобные:
[m]- 20x + 4 = 12\sqrt{(x + 3)^2 + y^2}[/m]
Делим левую и правую части на 4 и запишем корень слева:
[m]3\sqrt{(x + 3)^2 + y^2} = - 5x + 1[/m]
Снова возводим в квадрат:
9((x + 3)^2 + y^2) = (-5x + 1)^2
9(x^2 + 6x + 9 + y^2) = 25x^2 - 10x + 1
9x^2 + 54x + 81 + 9y^2 = 25x^2 - 10x + 1
Опять приводим подобные, переносим всё направо:
0 = 16x^2 - 64x - 80 - 9y^2
Выделяем полные квадраты и запишем 0 справа:
16(x^2 - 4x + 4 - 4) - 9y^2 - 80 = 0
16(x - 2)^2 - 64 - 9y^2 - 80 = 0
16(x - 2)^2 - 9y^2 = 144
Делим всё уравнение на 144 = 16*9, чтобы справа была 1:
[m]\large \frac{(x - 2)^2}{9} - \frac{y^2}{16} = 1[/m]
Это гипербола с центром A(2; 0) и полуосями a = 3, b = 4
Чертеж на рисунке 2.
12. Привести уравнение кривой к каноническому виду:
36x^2 + 49y^2 + 72x - 196y - 1442 = 0
Выделяем полные квадраты:
36(x^2 + 2x + 1 - 1) + 49(y^2 - 4y + 4 - 4) - 1442 = 0
36(x + 1)^2 - 36 + 49(y - 2)^2 - 196 - 1442 = 0
36(x + 1)^2 + 49(y - 2)^2 = 1674
Тут явная опечатка, должно получиться 1764 = 36*49.
Но тогда вместо 1442 должно было быть число 1532.
36(x + 1)^2 + 49(y - 2)^2 = 1764
Делим всё уравнение на 1764 = 36*49, чтобы справа получилась 1.
[m]\large \frac{(x+1)^2}{49} + \frac{(y-2)^2}{36} = 1[/m]
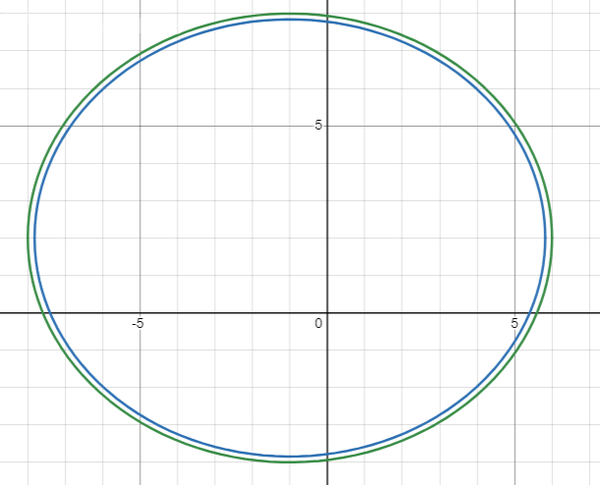
Это эллипс с центром B(-1; 2) и полуосями a = 7, b = 6
Но если все же опечатки нет, то берем начальное уравнение:
36(x + 1)^2 + 49(y - 2)^2 = 1674
И делим на 1674 = 2*3^3*31 = 9*186, чтобы справа получилась 1.
1674/36 = 18*3*31/36 = 93/2 = 46,5
А вот на 49 оно не делится никак.
[m]\large \frac{(x+1)^2}{46,5} + \frac{(y-2)^2}{1674/49} = 1[/m]
Это эллипс с тем же центром B(-1; 2) и полуосями
a = sqrt(46,5), b = sqrt(1674/49) = 3sqrt(186)/7
Чертеж обоих эллипсов на рисунке 3.
Внутренний - [m]\large \frac{(x+1)^2}{46,5} + \frac{(y-2)^2}{1674/49} = 1[/m]
Внешний - [m]\large \frac{(x+1)^2}{49} + \frac{(y-2)^2}{36} = 1[/m]