Задача 78897 Вычислить площадь фигуры, ограниченной...
Условие
математика ВУЗ
264
Решение
★
Сначала найдем пределы интегрирования, для этого приравняем функции:
3x^2 + 1 = 3x + 7
3x^2 - 3x - 6 = 0
x^2 - x - 2 = 0
(x - 2)(x + 1) = 0
x1 = -1; x2 = 2
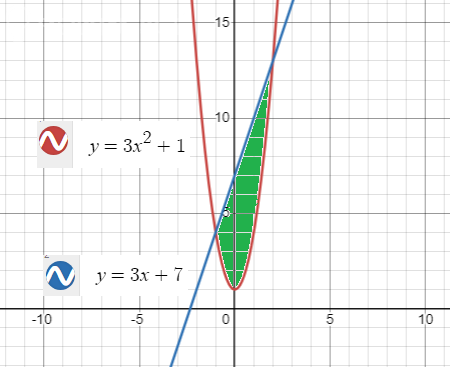
Кривые показаны на рисунке. Площадь заштрихована зеленым уветом.
Как видим, на этом отрезке прямая выше параболы, поэтому:
[m]S = \int \limits_{-1}^2 (3x + 7 - 3x^2 - 1) dx = \int \limits_{-1}^2 (-3x^2 + 3x + 6) dx = -x^3 + \frac{3x^2}{2} + 6x \Big |_{-1}^2 = [/m]
[m]= (-2^3 + \frac{3 \cdot 2^2}{2} + 6 \cdot 2) - (-(-1)^3 + \frac{3(-1)^2}{2} + 6(-1)) =[/m]
[m]= (-8 + 6 + 12) - (-(-1) + \frac{3}{2} - 6) = 10 - 1 - 1,5 + 6 = 13,5[/m]
Ответ: S = 13,5