Задача 76526 ...
Условие
13 Дано: ABCD — прямоугольник. Найдите расстояние от точки M до (ABCD).
10 Дано: точка O — середина MN. Докажите, что MO = MN_1 = NN_1.
14 Дано: ΔABC — правильный. Найдите расстояние от точки M до плоскости.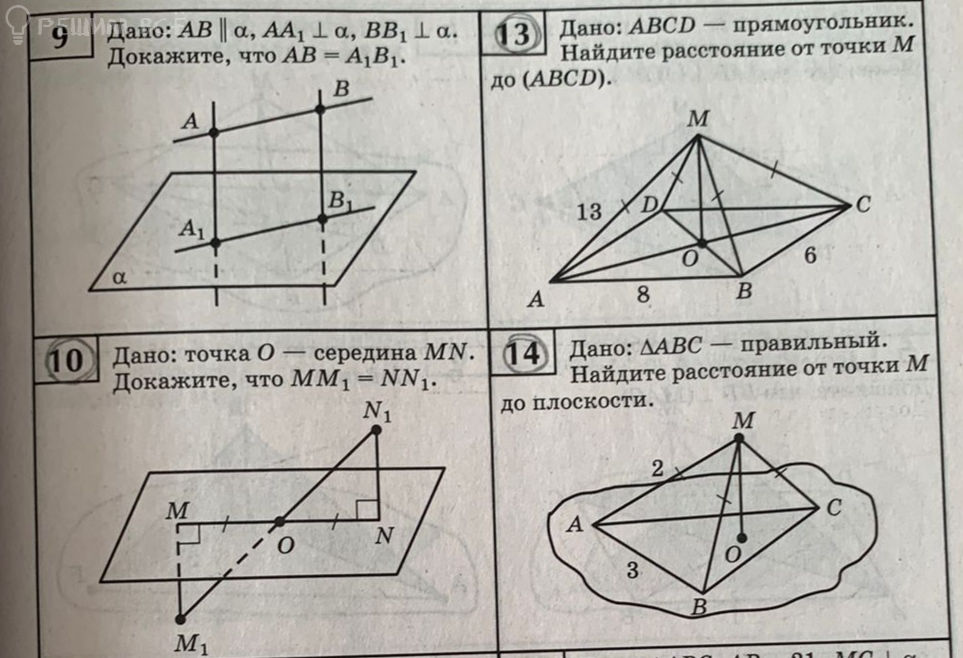
нет в списке колледж
601
Решение
★
Δ MM_(1)O=Δ NN_(1)O
под двум сторонам и углу между ними
⇒ MM_(1)= NN_(1)
13
MO^2=MA^2-AO^2
Так как
AO=(1/2)AC
Находим
AC^2=AB^2+BC^2=8^2+6^2=64=36=100
AC=10
AO=(1/2)AC=5
MO^2=MA^2-AO^2=13^2-5^2=169-25=144
[b]MO=12[/b]
14.
MO^2=MA^2-AO^2
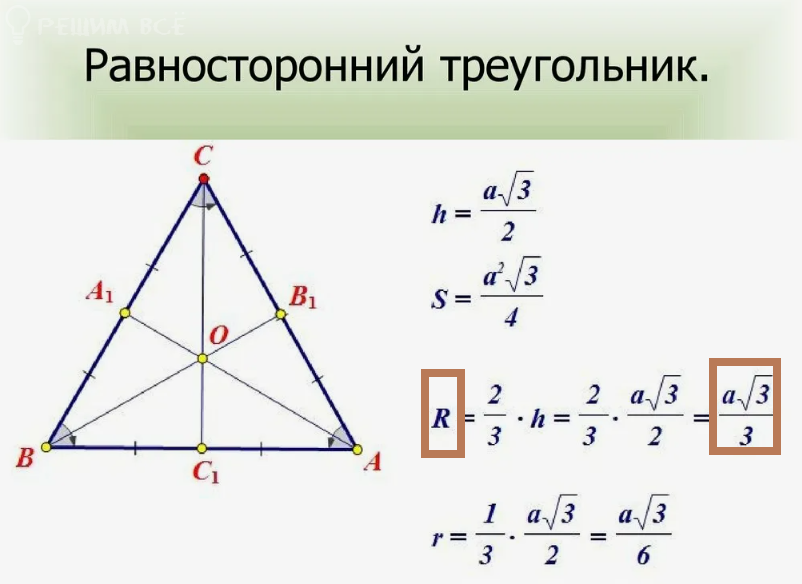
AO=BO=CO=R=a*sqrt(3)/3=3*sqrt(3)/3=sqrt(3)
MO^2=MA^2-AO^2=2^2-(sqrt(3))^2=4-3=1
[b]MO=1[/b]