Задача 63379 ...
Условие
1. ∫ (1 to ∞) dx / (x√(3x^2 - 2x - 1));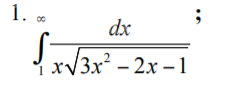
Решение
Несобственный интеграл второго рода, так как подынтегральная функция не определена в точке x=1.
Представим как сумму интегралов
[m]∫ _{1}^{+ ∞ }\frac{dx}{x\sqrt{3x^2-2x-1}}=∫ _{b}^{ +∞ }\frac{dx}{x\sqrt{3x^2-2x-1}}+∫ _{1}^{ b}\frac{dx}{x\sqrt{3x^2-2x-1}}[/m]
где
1 < b < + ∞.
Считаем [i] неопределенный [/i] интеграл:
[m]∫ \frac{dx}{x\sqrt{3x^2-2x-1}}[/m]
[m] \frac{1}{x}=t[/m] ⇒ [m] x=\frac{1}{t}[/m] ⇒ [m] dx=-\frac{1}{t^2}dt[/m]
[m]\sqrt{3x^2-2x-1}=\sqrt{3\cdot (\frac{1}{t})^2-2\cdot (\frac{1}{t})-1}=\frac{1}{t}\sqrt{3-2t-t^2}=[/m]
выделяем полный квадрат
[m]=\sqrt{4-(t^2+2t+1)}=\sqrt{4-(t+1)^2}[/m]
Тогда
[m]∫ \frac{dx}{x\sqrt{3x^2-2x-1}}=∫ \frac{-\frac{1}{t^2}dt}{\frac{1}{t}\cdot \frac{1}{t}\sqrt{3-2t-t^2}}=-∫ \frac{dt}{\sqrt{4-(t-1)^2}}[/m]
Табличный интеграл:
[m]=-∫ \frac{d(t-1)}{\sqrt{4-(t-1)^2}}=-arcsin\frac{t-1}{2}+C=-arcsin\frac{\frac{1}{x}-1}{2}+C[/m]
Рассматриваем первый интеграл
[m]I_{1}=∫ _{b}^{ +∞ }\frac{dx}{x\sqrt{3x^2-2x-1}}=lim_{A → +∞}∫ _{b}^{ A }\frac{dx}{x\sqrt{3x^2-2x-1}}=lim_{A → +∞}(- arcsin\frac{\frac{1}{x}-1}{2})|_{b}^{ A }=-arcsin(-\frac{1}{2})+arcsin\frac{\frac{1}{b}-1}{2}[/m]
Рассматриваем второй интеграл
[m]I_{2}∫ _{1}^{ b}\frac{dx}{x\sqrt{3x^2-2x-1}}=lim_{a → 1}∫ _{a}^{ b }\frac{dx}{x\sqrt{3x^2-2x-1}}=lim_{a → 1}(- arcsin\frac{\frac{1}{x}-1}{2})|_{a}^{ b }=arcsin\frac{\frac{1}{b}-1}{2}-arcsin 0[/m]
Таким образом
[m]∫ _{1}^{+ ∞ }\frac{dx}{x\sqrt{3x^2-2x-1}}=I_{1}+I_{2}=-arcisn (-\frac{1}{2})+arcsin\frac{\frac{1}{b}-1}{2}-arcsin\frac{\frac{1}{b}-1}{2}+arcsin 0=\\\\=[m]arcsin\frac{1}{2}+arcsin 0=\frac{π}{6}[/m]