Задача 63149 Составить уравнение плоскости,...
Условие
(2x - 2y + 3z - 4 = 0, 3x - y - z = 0)
и
(x + 2y - 4z + 1 = 0, x + y - 3z + 1 = 0).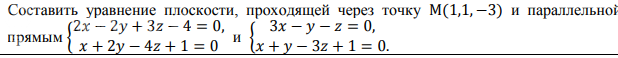
Решение
Пусть z=0
{2x-2y-4=0
{x+2y+1=0
Складываем
3x-3=0
x=1
y=-1
A(1;-1;0)
Пусть z=1
{2x-2y+3-4=0
{x+2y-4+1=0 ⇒
{2x-2y-1=0
{x+2y-3=0
3x=4
x=4/3
y=(2x-1)/2=((8/3)-1)/2=5/6
B(4/3; 5/6; 1)
vector{AB}=((4/3)-1; (5/6)-(-1); 1-0)=(1/3; 11/6; 1) - направляющий вектор первой прямо1
Аналогично находим направляющий вектор второй прямой
Пусть K(x;y;z) - произвольная точка плоскости.
Вектор vector{MK}=(x-1;y-1;z-(-3))=(x-1;y-1;z+3) лежит в искомой плоскости.
Три вектора компланарны.
Составляем определитель третьего порядка и приравниваем его к 0