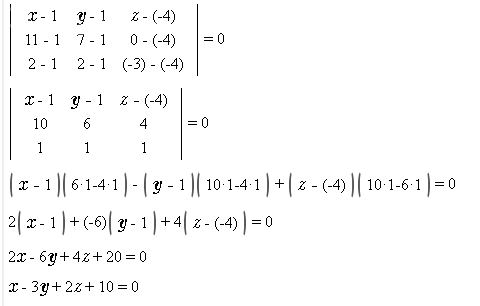Задача 61660 Найти уравнение плоскости, проходящей...

6197b89ccb163565984669c9

19.11.2021 21:29:31

Найти уравнение плоскости, проходящей через точки
A = (1;1;-4), B = (11;7;0), C = (2;2;-3) и записать его:

Найти параметрическое уравнение прямой, проходящей
через точки D = (-15;-7;-10) и E = (-1;0;-3).

{
x = + \cdot t
y = + \cdot t
z = + \cdot t
}

Найти координаты точки пересечения этой плоскости с этой прямой.

Ответ: __________________________________

Найти координаты проекции точки A = (-6,-1,3) на
прямую, проходящую через точки B = (-4,4,-3) и
C = (-5,2,-2).

Ответ: __________________________________

Найти координаты проекции точки A = (-7,-3,-9) на
плоскость, заданную уравнением -3x-2y-2z-11 = 0.

Ответ: __________________________________

5f3ea7e3faf909182968ddd9

19.11.2021 23:50:53

★

1.
Пусть M(x;y;z) - произвольная точка плоскости

vector{AM}=(x-1;y-1;z-(-4))
vector{AB}=(11-1;7-1;0-(-4))
vector{AC}=(2-1;2-1;-3-(-4))

компланарны.

Значит их смешанное произведение равно 0