Задача 61476 ...

60b77ffca1c50e1d3043a110

11.11.2021 00:49:14

13.29. Осевое сечение конуса — правильный треугольник АВС со стороной 1 см. Найдите длину кратчайшего пути по поверхности этого конуса из точки А в точку D — середину стороны ВС (рис. 13.17).

13.30. Крыша силосной башни имеет форму конуса. Высота крыши — 2 м. Диаметр основания башни — 6 м. Сколько листов кровельного железа потребовалось для покрытия крыши, если лист имеет размеры 0,7 м х 1,4 м, а на пивы идет 10% требуемости железа? (Примите π ≈ 3.)

5f3ea7e3faf909182968ddd9

11.11.2021 14:38:20

★

13.29.

Δ АСВ - осевое сечение конуса ( рис.1) - [i]равносторонний[/i]


S_(бок)=S_(сектора CAB)


S_(бок)=π*r*L

L=AC=BC=1

r=AB/2=1/2=0,5

⇒ S_(бок)=π*0,5*1=0,5π

S_(сектора CAB)=(π*R^2_(развертки))/2π)* ∠ ACB(рад)=(R/2)*∠ ACB(рад)

R=AC=BC=1

(R/2)*∠ ACB(рад)=0,5π
∠ ACB(рад)=π

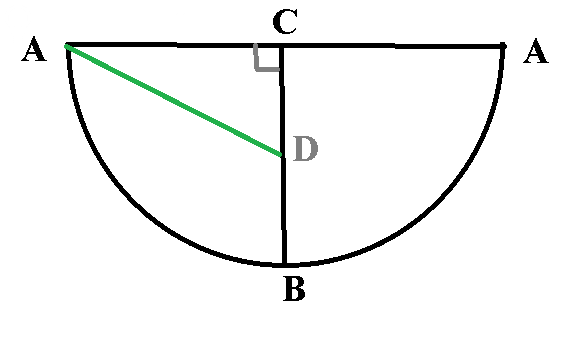
Значит развертка боковой поверхности конуса -[red] полуокружность [/red]

∠ АСD =90 °

AD^2=AC^2+CD^2=1+0,5^2=1+0,25=1,25

AD=sqrt(1,25)=sqrt(5/4)=sqrt(5)/2