Задача 61442 Исследовать на сходимость ряд №2...
Условие
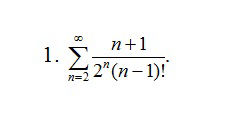
математика
173
Решение
★
[m]lim_{n → ∞ }\frac{a_{n+1}}{a_{n}}=lim_{n → ∞ }\frac{\frac{n+2}{2^{n+1}\cdot (n)!}}{\frac{n+1}{2^{n}\cdot (n-1)!}}=lim_{n → ∞ }\frac{(n+2)\cdot 2^{n}\cdot (n-1)!}{2^{n+1}\cdot n!\cdot(n+1)}=lim_{n → ∞ }\frac{n+2}{2n(n+1)}=0 < 1[/m]
сходится