Задача 61157 ...

615081977c1408291d4059c5

24.10.2021 17:10:42

1. Расположите данные числа tg(−8); 2 tg 8; tg 32 в порядке возрастания.
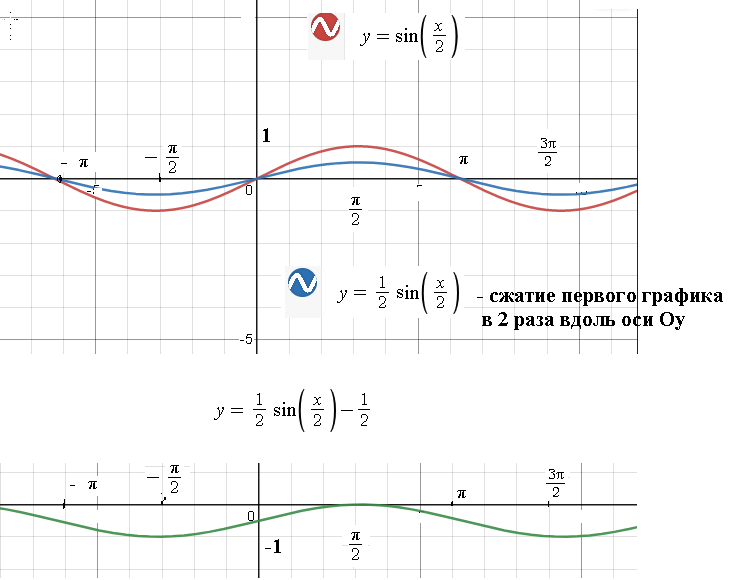
2. Для функции y = (1/2)sin(x/2) − 1/2; найдите:
a) область определения;
b) область значений.
3. Не выполняя построений, найдите для функции y = 2cos2x*cos3x + 2sin2x*sin3x
наименьший положительный период функции.
4. Построите график тригонометрической функции
a) нули функции;
b) асимптоты функции.
5. Исследуйте функцию на четность y = x^2 cos6x.
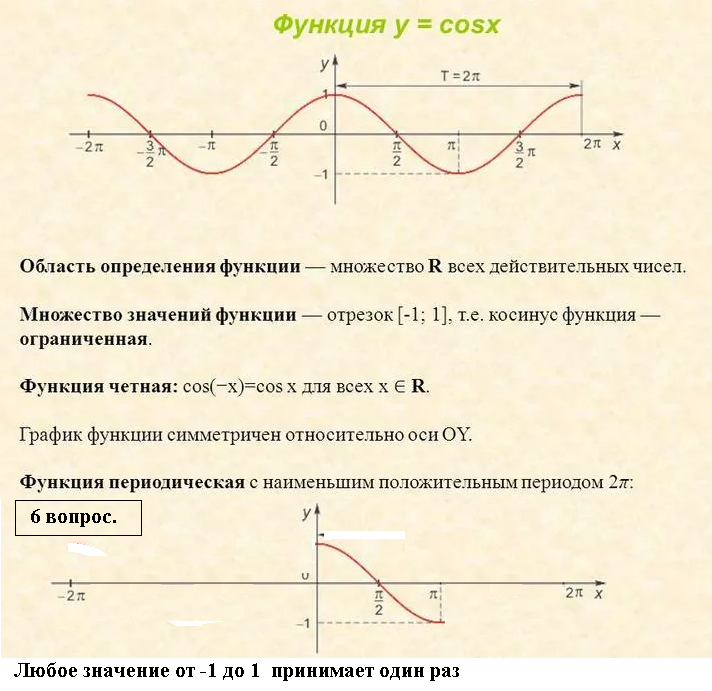
6. Какое значение функции y = cosx принимает на [0; π] ровно один раз?

5f3ea7e3faf909182968ddd9

24.10.2021 21:42:08

★

1.


π радиан = 180 ° ⇒ 1 радиан= (180/π) °

8 радиан =8* (180/π) ° > 450°

поэтому угол в 8 радиан расположен во второй четверти

Тангенс во второй четверти отрицательный

tg 8 <0

Тангенс - нечетная функция

tg (-8)=-tg8 >0


2,6 радиан тоже во второй четверти.

tg 2,6 <0

32 радиан=32* (180/π) ° в первой четверти



tg2,6< tg 8 < tg32 < tg 8




2.
Область определения (- ∞ :+ ∞)

-1 ≤ sin(x/2) ≤ 1

-1/2 ≤ (1/2)*sin(x/2) ≤ 1/2

-1/2 -(1/2)≤ (1/2)*sin(x/2) -(1/2)≤ 1/2-(1/2) ⇒

-≤ (1/2)*sin(x/2) -(1/2)≤0

[-1;0] - область изменения

3.

2cos2x*cos3x+2sin2x*sin2x=2*(cos2x*cos3x+sin2x*sin3x)=2*cos(2x-3x)=2cos(-x)=2cosx

cos(-x)=cosx по свойству четности косинуса


Т=2π


4.

5.
f(x)=x^2*cos6x
Четная.
По определению:

1) Область определения (- ∞ :+ ∞) - симметричная относительно нуля

2)

f(-x)=(-x)^2*cos(6*(-x))=x^2*cos6x

f(-x)=f(x)