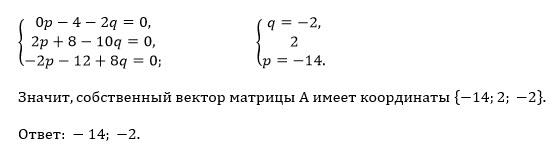Задача 60915 ...
Условие
A =
[−6 −2 −2]
[ 2 −2 −10]
[−2 −6 2]
Вычислите, какое из чисел λ = −6 или λ = −5 является собственным числом матрицы A.
Найдите собственный вектор, отвечающий этому собственному числу.
Собственный вектор запишите в виде {p; 2; q}
В ответ введите числа р и q, разделив их точкой с запятой.
Решение
[m]\begin {vmatrix} -6- λ &-2&-2\\2&-2- λ &-10\\-2&-6&2- λ \end {vmatrix}=0[/m]
Подставив (-6) получим:
[m]\begin {vmatrix} -6- (-6) &-2&-2\\2&-2-(-6) &-10\\-2&-6&2- (-6) \end {vmatrix}=0[/m]
Считаем определитель:
[m]\begin {vmatrix} 0 &-2&-2\\2&4 &-10\\-2&-6&8 \end {vmatrix}=[/m]
получаем 0 ( см. скрин)
λ =-6 является собственным числом
Подставив (-5) получим:
[m]\begin {vmatrix} -6- (-5) &-2&-2\\2&-2-(-5) &-10\\-2&-6&2- (-5) \end {vmatrix}=0[/m]
Считаем определитель:
[m]\begin {vmatrix} -1 &-2&-2\\2&3 &-10\\-2&-6&7 \end {vmatrix}=39 ≠0 [/m]
λ =-5 не является собственным числом 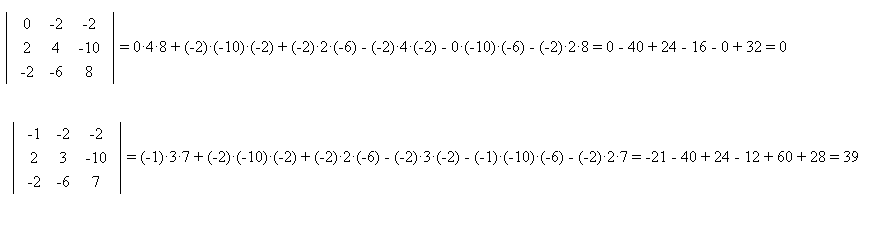
Все решения