Задача 60623 12. Решите систему уравнений: 1) {x^2 -...
Условие
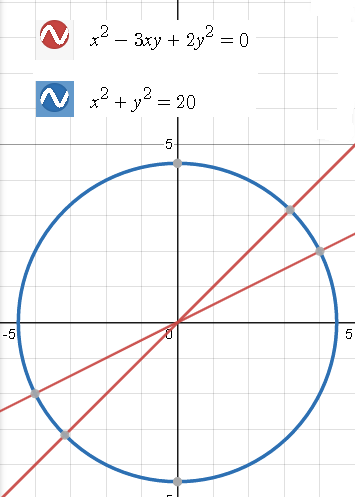
1) {x^2 - 3xy + 2y^2 = 0,
x^2 + y^2 = 20;
2) {x^2 - 5y^2 + 1 = 0,
3xy + 7y^2 = 1;
3) {x^2 - 4xy + y^2 - 6 = 0,
4 + 3xy - y^2 = 0.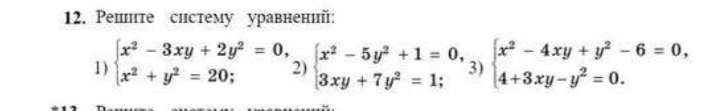
Решение
Решаем способом деления, т.е заменим одно уравнение частным двух других уравнений и получим систему:
[m]\left\{\begin {matrix}\frac{x^2-4xy+y^2}{y^2-3xy}=\frac{6}{4}\\4+3xy-y^2=0\end {matrix}\right.[/m]
Первое уравнение представляет собой пропорцию. Находим произведение крайних и средних членов пропорции:
[m]\left\{\begin {matrix}4\cdot (x^2-4xy+y^2)=6\cdot (y^2-3xy)\\4+3xy-y^2=0\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}4x^2-16xy+4y^2=6y^2-18xy\\4+3xy-y^2=0\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}4x^2+2xy-2y^2=0\\4+3xy-y^2=0\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}2x^2+xy-y^2=0\\4+3xy-y^2=0\end {matrix}\right.[/m]
Первое уравнение однородное , второго порядка . Делим на y^2. Применяем замену переменной [m]\frac{x}{y}=t[/m]
и получаем квадратное уравнение : [m]2t^2+t-1=0[/m] D=9
[m]t_{1}=-1[/m]; [m]t_{2}=\frac{1}{2}[/m]
Обратный переход и две системы:
[m]\left\{\begin {matrix}\frac{x}{y}=-1\\4+3xy-y^2=0\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}\frac{x}{y}=\frac{1}{2}\\4+3xy-y^2=0\end {matrix}\right.[/m]
Способ подстановки и:
[m]\left\{\begin {matrix}x=-y\\4+3\cdot (-y)\cdot y-y^2=0\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}2x=y\\4+3x\cdot 2x-(2x)^2=0\end {matrix}\right.[/m]
....
2)
Решаем способом сложения, т.е заменим одно уравнение суммой двух данных уравнений и получим систему:
[m]\left\{\begin {matrix}x^2+3xy+2y^2=0\\3xy+7y^2=1\end {matrix}\right.[/m]
Далее решаем так как 1)
[m]\left\{\begin {matrix}x^2+2xy+xy+2y^2=0\\3xy+7y^2=1\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}(x^2+2xy)+(xy+2y^2)=0\\3xy+7y^2=1\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}(x+2y)(x+y)=0\\3xy+7y^2=1\end {matrix}\right.[/m] ⇒
[m]\left\{\begin {matrix}(x+2y)=0\\3xy+7y^2=1\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}(x+y)=0\\3xy+7y^2=1\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x=-2y\\3xy+7y^2=1\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}x=-y\\3xy+7y^2=1\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x=-2y\\3\cdot (-2y)\cdot y+7y^2=1\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}x=-y\\3\cdot(-y)\cdot y+7y^2=1\end {matrix}\right.[/m]
....
1)
Разложим первое уравнение системы на множители:
[m]\left\{\begin {matrix}x^2-2xy-xy+2y^2=0\\x^2+y^2=20\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}(x^2-2xy)-(xy-2y^2)=0\\x^2+y^2=20\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x(x-2y)-y(x-2y)=0\\x^2+y^2=20\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}(x-2y)(x-y)=0\\x^2+y^2=20\end {matrix}\right.[/m]
Произведение равно 0 когда хотя бы один из множителей равен 0
[m]\left\{\begin {matrix}(x-2y)=0\\x^2+y^2=20\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}(x-y)=0\\x^2+y^2=20\end {matrix}\right.[/m]
Решаем каждую систему [i] способом подстановки[/i] и получаем четыре решения.
[m]\left\{\begin {matrix}x=2y\\(2y)^2+y^2=20\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}x=y\\y^2+y^2=20\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x=2y\\5y^2=20\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}x=y\\2y^2=20\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x=2y\\y^2=4\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}x=y\\y^2=10\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x=2y\\y_{1}= 2\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}x=y\\y_{3}= \sqrt{10}\end {matrix}\right.[/m]
ИЛИ
[m]\left\{\begin {matrix}x=2y\\y_{2}= - 2\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}x=y\\y_{4}=- \sqrt{10}\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x_{1}=2\cdot 2 \\y_{1}= 2\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}x_{3}=\sqrt{10}\\y_{3}= \sqrt{10}\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x_{2}=2\cdot (-2) \\y_{1}= -2\end {matrix}\right.[/m] ИЛИ [m]\left\{\begin {matrix}x_{3}=-\sqrt{10}\\y_{3}=- \sqrt{10}\end {matrix}\right.[/m]
Cм. также графическое решение системы: