Задача 60582 ...

61018b3ba1c50e1d30443518

27.08.2021 18:47:43

Из вершины А, большего основания AD трапеции ABCD, восставлен перпендикуляр, который пересекается с продолжением стороны CD в точке К. Найдите меньшее основание трапеции, если АК=10 см, ∠КАВ=30°, ∠АКD=45° и высота трапеции равна 2√3 см.

A) (2√3−5) см
B) 6√2 см
C) (8−2√3) см
D) 3√5 см
E) 14 см

5f3ea7e3faf909182968ddd9

27.08.2021 22:34:38

∠ KAD=90 ° ⇒ AKD - прямоугольный

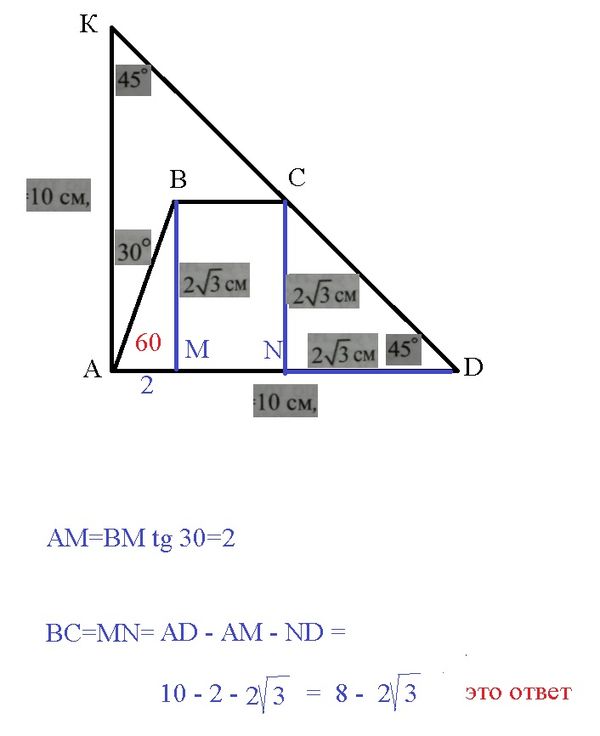
∠ AKC=45 ° ⇒ AKD - прямоугольный равнобедренный AK=[b]AD=10[/b]



∠ ADC=45 °

BM ⊥ AD; CN⊥ AD

BM=CN=2sqrt(3)

⇒ ND=2sqrt(3)


Из прямоугольного треугольника АВМ

tg ∠ BAM= BM/AM ⇒

AM=BM/tg60 °=BM*tg30 ° =2sqrt(3)*(sqrt(3)/3)=[b]2[/b]