Задача 59799 Второе задание, кто сможет)...
Условие
математика ВУЗ
558
Решение
★
ε = 0,4
σ = 2
n = x^(2)σ^(2)/ε^(2)
2Ф(x) = γ
2Ф(x) = 0,975
Ф(x) = 0,975/2 = 0,4875
По таблице функции Ф(x) (см. картинку)
x = 2,24
n = 2,24^(2)*(2^(2)/0,4^(2)) = 125,44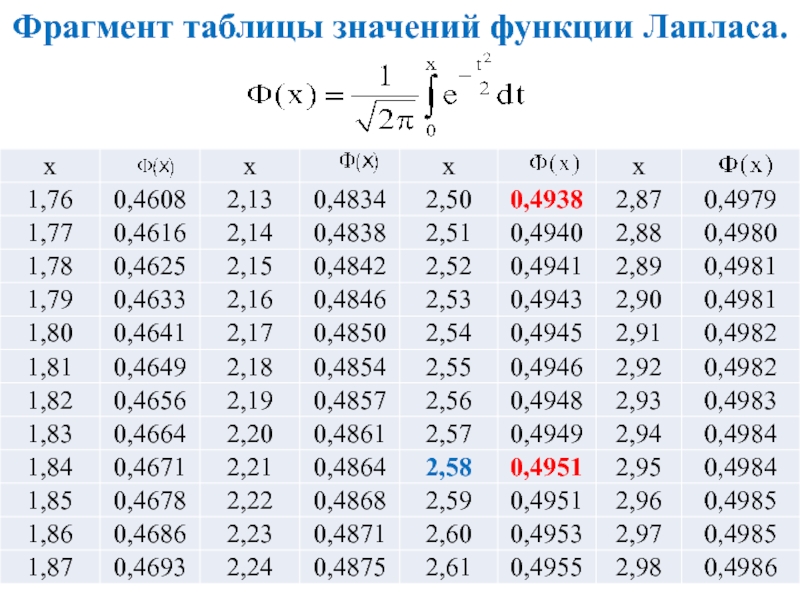
Ответ: n = 126