Задача 58342 18. Построить несколько точек эллипса ...

60434963c87bcc1c7d522cf2

06.03.2021 13:33:33

18. Построить несколько точек эллипса x^2/25 + y^2/9 = 1
19. Упростить уравнение параболы y = 5x^2 + 4x - 3, найти координаты вершины и величину параметра p. Начертить эскиз кривой.

5f3ea7e3faf909182968ddd9

06.03.2021 15:08:22

★

1) a=5; b=3

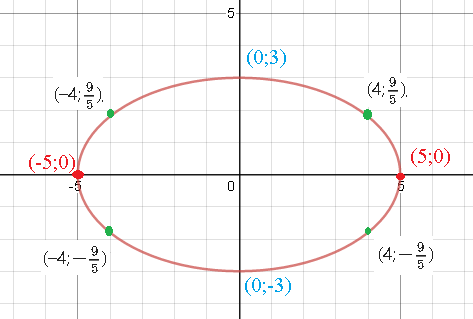
(5;0);(-5;0);(0;3);(0;-3) - вершины эллипса.


[m]y^2=9\cdot (1-\frac{x^2}{25})[/m]

x=4 ⇒ [m]y^2=9\cdot (1-\frac{4^2}{25})[/m] ⇒ [m]y^2=\frac{81}{25}[/m] ⇒ [m]y= ± \frac{9}{5}[/m]

Поэтому точки:

(4;[m]\frac{9}{5}[/m]); (-4;[m]\frac{9}{5}[/m]); (4;[m]-\frac{9}{5}[/m]); (-4;[m]-\frac{9}{5}[/m]) принадлежат эллипсу.


2)
Выделить полный квадрат:

[m]y=5(x^2+\frac{4}{5}-\frac{3}{5})[/m]

[m]y=5((x+\frac{2}{5})^2-\frac{4}{25}-\frac{3}{5})[/m]

[m]y=5((x+\frac{2}{5})^2-\frac{19}{25})[/m]

[m]y=5(x+\frac{2}{5})^2-\frac{19}{5}[/m]

Вершина в точке [m](\frac{2}{5};-\frac{19}{5})[/m]

2p=5

[b]p=2,5[/b]