Задача 58073 2. Вычислите пределы функции: [m]...

6035546716e9eb62f3f7733c

23.02.2021 22:16:10

2. Вычислите пределы функции:

[m] \lim_{x \to 1} \frac{x^{2} - 8x + 7}{x - 1}[/m]

[m] \lim_{x \to 2} \frac{7 - 6x^{2}}{2 + 3x^{2}}[/m]



3. Исследуйте функцию и постройте её график:

15. [m] y = x^{3} - 4x^{2} + 3x[/m]

5f3ea7e3faf909182968ddd9

24.02.2021 00:24:35

★

10.
a)
[m]\lim_{x \to 1 }\frac{x^2-8x+7}{x-1}=\frac{1-8+7}{1-1}=\frac{0}{0}=[/m]

неопределенность.

Раскладываем на множители числитель :

[m]=\lim_{x \to 1 }\frac{(x-1)(x-7)}{x-1}=[/m]

сокращаем на [m](x-1)[/m]

[m]=\lim_{x \to 1 (}x-7)=1-7=-6[/m]

б)

[m]\lim_{ \to \infty }\frac{7-6x^2}{2+3x^2}=[/m]

Неопределенность ( ∞ / ∞ )

Делим числитель и знаменатель на x^2:

[m]=\lim_{ \to \infty }\frac{\frac{7-6x^2}{x^2}}{\frac{2+3x^2}{x^2}}=[/m]

Делим почленно, те каждое слагаемое числителя делим на [m]x^2[/m] и
каждое слагаемое знаменателя делим на [m]x^2[/m]:

[m]=\lim_{ \to \infty }\frac{\frac{7}{x^2}-\frac{6x^2}{x^2}}{\frac{2}{x^2}+\frac{3x^2}{x^2}}=[/m]

[m]=\lim_{ \to \infty }\frac{\frac{7}{x^2}-6}{\frac{2}{x^2}+3}=\frac{0-6}{0+3}=-2[/m]



15.
Область определения (- ∞ ;+ ∞ )

f`(x)=(x^3-4x:^2+3x)`

f`(x)=3x^2-8x+3


f`(x)>0

3x^2-8x+3>0

D=64-36=28

x_(1,2)=(8 ± 2sqrt(7))/6=(4 ± sqrt(7))/3

f`(x)>0 на (- ∞ ; (4 - sqrt(7))/3) и на ((4 + sqrt(7))/3;+∞ )

значит функция возрастает на (- ∞ ; (4 - sqrt(7))/3) и на ((4 + sqrt(7))/3;+∞ )


f`(x)<0 на ( (4 - sqrt(7))/3);(4 + sqrt(7))/3 )

значит функция убывает на ( (4 - sqrt(7))/3);(4 + sqrt(7))/3 )

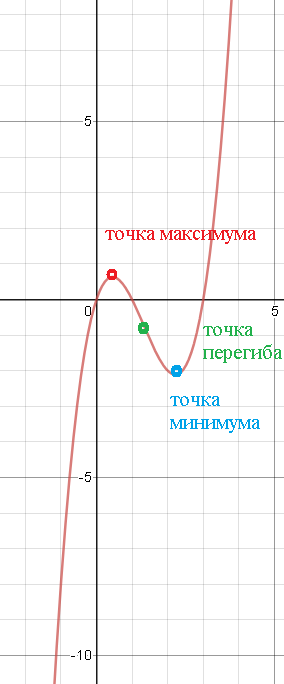
график см. рис.